Извесны два угла треугольника АВС найдите его третий угол , угожите вид треугольника и заполните пропуски

Извесны два угла треугольника АВС найдите его третий угол , угожите вид треугольника и заполните про

👇

Увидеть ответ

Ответ:

milka1951

07.05.2023

1. 130. 25. 25. Тупоугольный

2. 75. 80. 25. Остроугольный

3. 120. 10. 50. Тупоугольный

4. 80. 90. 10. Прямоугольный

5. 45. 45. 90. Прямоугольный

6. 80. 80. 20 остроугольный

Объяснение:

4,8(80 оценок)

Ответ:

simkinaalinoschka

07.05.2023

1)180-(130+25)=25

2)180-(75+80)=25

3)180-(10+50)=120

4)180-(80+10)=90

5)180-(90+45)=145

6)180-(80+20)=80

4,6(60 оценок)

Открыть все ответы

Ответ:

dodpddpfp

07.05.2023

Треугольник АВС и треугольник А1В1С1 равны по стороне и двум прилежащим к ней углам. Отрываем треугольник АВС. Точку А совмещаем с точкой А1. Луч АС совмещаем с лучом А1С1. Но отрезок АС равен отрезку А1С1. А на данной полупрямой от её начала можно отложить только один отрезок данной линейной меры, значит, точка С совпадет с точкой С1. Но угол А равен углу А1, а от данной полупрямой в данной полуплоскости можно отложить только один угол данной градусной меры, значит луч АВ пойдёт по лучу А1В1. Но угол С равен углу С1, а от данной полупрямой в данной полуплоскости можно отложить только один угол данной градусной меры, значит луч ВС пойдёт по лучу В1С1. А две прямые пересекаются только в одной точке. Лучи АВ и ВС и лучи А1В1 и В1С1 пресекутся в одной точке. Треугольники совпали всеми своими точками. Значит они равны. Теорема доказана

4,5(7 оценок)

Ответ:

Poli4ka228

07.05.2023

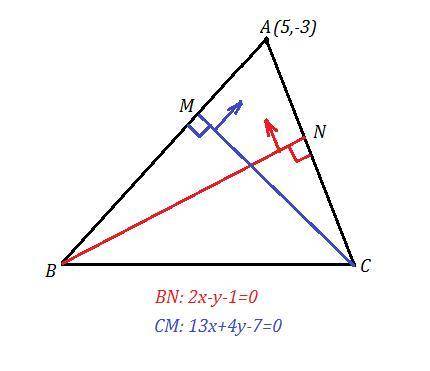
Проверим, лежит ли точка А(5,-3) на какой-либо заданной высоте. Подставим координаты этой точки в уравнения высот. Если равенство получим верное, то точка лежит на прямой.

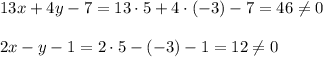
$13x+4y-7=13\cdot 5+4\cdot (-3)-7=46\ne 0\\\\2x-y-1=2\cdot 5-(-3)-1=12\ne 0$

Точка А(5,-3) не лежит ни на одной высоте. Для определённости, пусть высота BN имеет уравнение 2х-у-1=0, а высота СМ: 13х+4у-7=0.

BN⊥AC ⇒ направляющий вектор для АС равен нормальному вектору для BN: $\vec{s}_{AC}=(2,-1)$ .

Точка А(5,-3)∈АС и уравнение АС имеет вид:

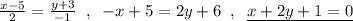
$\frac{x-5}{2}=\frac{y+3}{-1}\; \; ,\; \; -x+5=2y+6\; \; ,\; \; \underline {x+2y+1=0}$

CM⊥AB ⇒ направляющий вектор для АВ равен нормальному вектору для CМ: $\vec{s}_{AB}=(13,4)$ .

Точка А(5,-3)∈АВ и уравнение АВ имеет вид:

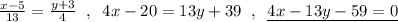
$\frac{x-5}{13}=\frac{y+3}{4}\; \; ,\; \; 4x-20=13y+39\; \; ,\; \; \underline {4x-13y-59=0}$

Координаты точки В найдём как точку пересечения АВ и BN, а координаты точки С найдём как точку пересечения АС и CM .

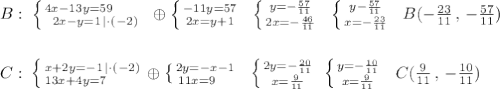
$B:\; \left \{ {{4x-13y=59\qquad } \atop {2x-y=1\, |\cdot (-2)}} \right.\oplus \left \{ {{-11y=57} \atop {2x=y+1}} \right. \; \; \left \{ {{y=-\frac{57}{11}} \atop {2x=-\frac{46}{11}}} \right.\; \; \left \{ {{y-\frac{57}{11}} \atop {x=-\frac{23}{11}}} \right. \; \; B(-\frac{23}{11}\, ,\, -\frac{57}{11})\\\\\\C:\; \left \{ {{x+2y=-1\, |\cdot (-2)} \atop {13x+4y=7\qquad }} \right.\oplus \left \{ {{2y=-x-1} \atop {11x=9\quad }} \right. \; \; \left \{ {{2y=-\frac{20}{11}} \atop {x=\frac{9}{11}}} \right.\; \left \{ {{y=-\frac{10}{11}} \atop {x=\frac{9}{11}}} \right.\; \; C(\frac{9}{11}\, ,\, -\frac{10}{11})$