Обозначим (начиная с нижнего левого острого угла) по часовой стрелке ABCD. Тогда AD = 12 см и AB=8 см Высоты из угла В - на AD - BE и на CD - BF <EBF = 60 BE - высота, т. е. BE перпендикулярно AD, значит BD перпендикулярно и BC, т.к. BC параллельно AD, следовательно, < CBE - прямой и <CBF =90 - <EBF =90-60 =30 BF - высота, она перпендикулярна CD, т.е. треугольник BFC - прямоугольный, значит <BCF = 90 - <CBF = 90 -30 =60 Но <A = < C, значит <A =60 и можем найти высоту BE из треугольника AEB BE=AB* cos <A BE = 8*cos 60 = 8* корень(3)/2 = 4*корень(3) площадь параллелограмма равна произведению основания на высоту
S = AD*BE = 12*4*корень(3) = 48 * корень(3) кв. см
№1: . №2:
. №2: 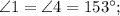
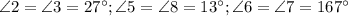 .
.
Объяснение:№1.
Пусть , тогда
, тогда  - секущая.
- секущая.
Теорема: "При пересечении двух параллельных прямых секущей, сумма односторонних углов равна .
.
№2.
Обозначим данные прямые буквами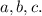
Пусть - секущая прямых
- секущая прямых  и
и 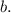
Теорема: "При пересечении двух параллельных прямых секущей, накрест лежащие углы равны".
============================================================
Свойство: "Вертикальные углы равны".
Свойство: "Сумма смежных углов равна ".
".
Рассмотрим углы, образовавшиеся при пересечении прямых и
и 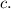
===========================================================
Рассмотрим углы, образовавшиеся при пересечении прямых и
и  .
.