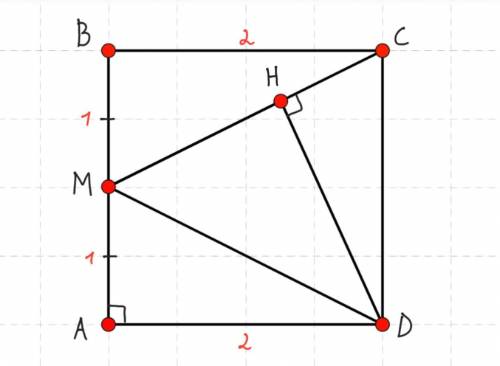
Дано: ABCD — квадрат, Sabcd= 4, т.М — середина АВ, АМ=ВМ, DH⟂СМ.
Найти: DH.
Решение.
1) Найдем сторону квадрата.
АВ²= 4;
АВ= 2 (–2 не подходит).
AB=BC=CD=AD= 2.
т.M — середина АВ, значит, АМ=ВМ= 2:2= 1.
2) Мы видим два равных прямоугольных треугольника: ΔMBC и ΔMAD (равны по двум катетам).
Найдем их площадь. Площадь прямоугольного треугольника равна половине произведения его катетов.
Значит, Smbc= Smad= ½•1•2= 1.
3) А площадь треугольника MDC равна разности площади квадрата и площадей треугольников MBC и MAD.
Т.е. Smdc= Sabcd–Smbc–Smad= 4–1–1= 4–2= 2.
4) Найдем сторону МС прямоугольного треугольника МВС (МС - это гипотенуза) по т.Пифагора:
МС²= МВ²+ВС²;
МС²= 1+2²;
МС²= 5;
МС= √5
5) Площадь обычного (произвольного) треугольника равна произведению половины основания этого треугольника на высоту, проведённую к этому основанию.
Для треугольника MDC это выглядит так:
Smdc= ½•MC•DH.
2= ½•√5•DH;
2 : ½ = √5DH;
√5DH= 4;
DH= 4/√5.
Расстояние от вершины D квадрата ABCD до прямой СМ равно 4/√5.
ОТВЕТ: 4/√5.
Для любого треугольника справедлива теорема синусов, которая говорит о следующем:
A/sin(a)=B/sin(b)=C/sin(c)=2R, где:
A/sin(a)=B/sin(b)=C/sin(c) - соотношения сторон треугольников к синусу противоположных им углов;
R - радиус окружности, описанной около треугольника.
1). Имеем сторону треугольника 3 (см) и противоположный ей угол, равный 120°. Тогда по теореме синусов:
3/sin(120°)=2R;
3/sin(90°+30°)=2R;
3/cos30°=2R;
3/(√3/2)=2R;
6/√3=2R;
R=3/√3; | освободимся от иррациональности, домножим и числитель, и знаменатель на √3
R=√3.
2). Аналогично, имеем сторону 3 см и угол, равный 30:
3/sin(30°)=2R;
3/(1/2)=2R;
6=2R;
R=3.
3). Аналогично, имеем сторону 3 см и угол, равный 135°;
3/sin(135°)=2R;
3/sin(90°+45°)=2R;
3/cos45°=2R;
3/(√2/2)=2R;
6/√2=2R;
R=3/√2; | освободимся от иррациональности, домножим и числитель, и знаменатель на √2
R=(3*√2)/2.
ответ: 1). R=√3; 2). R=3; 3). R=(3*√2)/2.