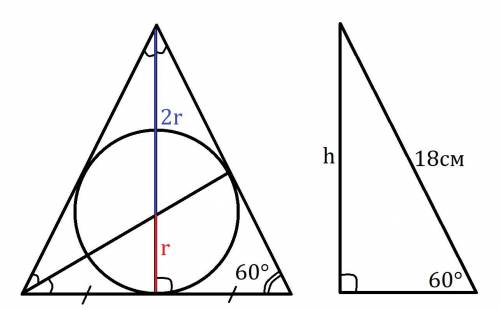
Центр вписанной окружности лежит на пересечении биссектрис. В правильном треугольнике биссектриса это ещё медиана и высота. Медианы в треугольнике делятся точкой пересечения в отношении 2 к 1, считая от вершины. Таким образом радиус (r) вписанной окружности это треть от высоты треугольника.
Высота (h) правильного треугольника со стороной 18см:
h = 18·sin60° = 18·(√3)/2 = 9√3 см
r = h/3 = (9√3)/3 = 3√3 см
ответ: 3√3 см.
Можно так же вывести формулу связи радиуса (r) вписанной в правильный треугольник окружности и стороны (а) треугольника.
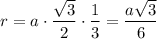
8² = 4² + x²
64 = 16 + x²
x² = 48
x = √48
Т.к. ромб это частный случай параллелограмма, то для него справедлива формула S = ah
Sромба = √48 · 8 = √ 48 · √64 = √3072 = 32√3 см²