Объяснение:
Рассмотрим линейную функцию y = 3 ∙ x, определенную на числовом отрезке [−2; 3]. Эта функция является прямой пропорциональностью с угловым коэффициентом k = 3, графиком которой является прямая линия, проходящая через начало координат. Так как k < 0, то функция y = − 3 ∙ x является убывающей, то есть большему значению аргумента соответствует меньшее значение функции:
х = 3 – наибольшее значение аргумента на числовом отрезке [−2; 3];
y = 3 ∙ 3 = 9 − наименьшее значение линейной функции y = 3 ∙ x на отрезке [−3; 3].
ответ: 9 − наименьшее значение линейной функции y = 3 ∙ x на отрезке [−3
Нехай задана правильна трикутна призма, бічні грані якої є квадратами, а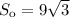 см² — площа основи цієї призми.
см² — площа основи цієї призми.
Основа призми є правильним (рівностороннім) трикутником зі строною см. Знайдемо цю сторону, скориставшись площею рівностороннього трикутника:
см. Знайдемо цю сторону, скориставшись площею рівностороннього трикутника: 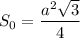
Отже,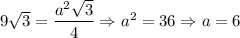 см.
см.
Через те що бічні грані є квадратами, тоді ребра призми дорівнюють 6 см (за властивістю квадрата) — ребра правильної призми є висотою призми.
Об'єм правильної трикутної призми можна розрахувати за формулою
Знайдено значення шуканої величини:
Відповідь: А)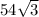 см³
см³