
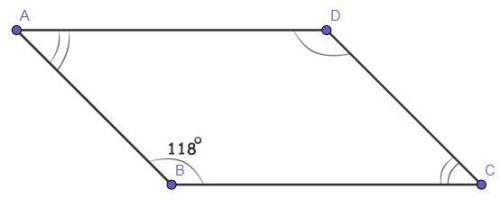
Четырёхугольник ABCD - параллелограмм.
∠В - тупой.
∠В = 118°.
Найти :Острый угол параллелограмма = ?
Решение :Если в параллелограмме имеется один тупой угол, то в этом параллелограмме есть ещё один тупой угол и два острых угла.Нам дан один тупой угол - это ∠В. А как теперь понять какой ещё тупой угол в этом параллелограмме?
А дело в том, что -
В параллелограмме противоположные углы равны.На рисунке ∠В = ∠D = 118°.
Тогда остаётся, что ∠А = ∠С - острые.
Сумма внутренних углов любого четырёхугольника равна 360°.То есть -
∠А + ∠В + ∠С + ∠D = 360°
∠А + ∠C = 360° - ∠В - ∠D
∠А + ∠C = 360° - 118° - 118°
∠А + ∠C = 124°
∠A = ∠C = 124° : 2 = 62°.
ответ :62°.
Внимание : тут два варианта .
56 или 52 см
Объяснение:
Вариант 1 (если бисс АК)
1) уг 1=уг 2 (как накрест лежащие при парал прямых);
уг 1=уг 3 (тк бисс);
тогда уг 2=уг3 => треуг АВК–равнобед =>АВ=ВК=10 и =СD (как стороны парал);
2) ВС=18+10=28=АD;
3) Р =( 18+10)*2=56 см
Вариант 2 (если бисс DК)
1) уг 1=уг 2 (как накрест лежащие при парал прямых);
уг 1=уг 3 (тк бисс);
тогда уг 2=уг3 => треуг DСК–равнобед =>DС=СК=8 и =АВ (как стороны парал);
2) ВС=18+8=26=АD;
3) Р =( 18+8)*2=52
Чертёж в приложении.
Если что-то непонятно , пишите в комментах.
Успехов в учёбе! justDavid