8 см ; 16 см
Объяснение:
Ширина а=х см
Длина b= 2х
Р=48
Р=2a+2b
48=2X+2×2X
48=2X+4X
48=6X
X=8
Ширина а=8 см
Длина b=2×8=16 cм
ответ: l²=34
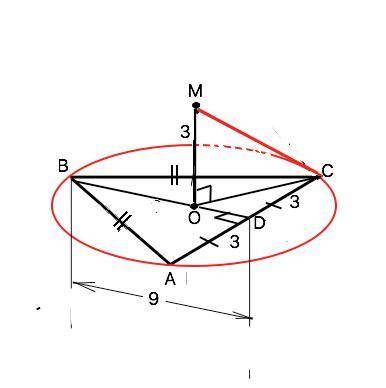
Объяснение: Точка M равноудалена от всех вершин данного треугольника, следовательно, все наклонные из М к вершинам, а, значит, и к плоскости треугольника, равны, поэтому равны и их проекции ОС=ОВ=ОА и равны радиусу описанной около ∆ АВС окружности.
Искомое расстояние МС - гипотенуза прямоугольного ⊿ МОС. Для её нахождения нужно найти катет ОС этого треугольника. ОС=R.
Формула радиуса описанной окружности R=a•b•c/4S ( где а, b и с - стороны треугольника).
S=BD•AC:2=9•6:2=27
Боковые стороны ∆ (АВС) найдём из ⊿ АВD. Высота ВD в равнобедренном треугольнике ещё и медиана (свойство)
По т.Пифагора. АВ=√(BD²+AD²)=√(9²+3²)=√90
R=(√90•√90•6):4•27= 5
ОС=5 ⇒ МС²=(MO²+OC²)=3²+5²=34 ⇒ l²=34
По теореме Пифагора:
АВ² = АС² + СВ² = 15² + 8² = 225 + 64 = 289
АВ = √289 = 17
Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе.
Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.
Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему.
sin∠A = BC / AB = 8/17
cos∠A = AC / AB = 15/17
tg∠A = BC / AC = 8/15
sin∠B = AC / AB = 15/17
cos∠B = BC / AB = 8/17
tg∠B = AC / BC = 15/8
8 и 6
Объяснение:
одна сторона - х, вторая сторона 2х
подставляем в формулу Р=2(a+b)
48 = 2*(x + 2x)
имеем: 48 = 2* 3x
оттуда, х = 48: 6
x = 8 (2*8=16)
ответ: 8 и 16