
ответ: 16√2
Объяснение:
Сумма углов трапеции, прилежащих к одной боковой стороне, равна 180°.
∠BCD + ∠CDA = 180°
∠CDA = 180° - ∠BCD = 180° - 150° = 30°
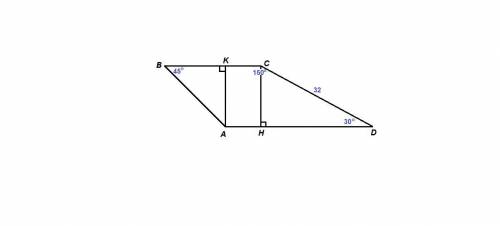
Проведем высоты СН и АК.
ΔCHD: ∠CHD = 90°,
СН = 1/2 CD = 1/2 · 32 = 16, по свойству катета, лежащего против угла в 30°.
АК = СН = 16 как высоты трапеции.
ΔАВК: ∠АКВ = 90°,
∠ВАК = 90° - ∠АВК = 45°, так как сумма острых углов прямоугольного треугольника равна 90°.
∠АВК = ∠ВАК = 45°, ⇒ ΔАВК равнобедренный, значит
ВК = АК = 16.
По теореме Пифагора:
АВ = √(АК² + ВК²) = √(16² + 16² ) = √(16² · 2) = 16√2
Так как у ромба все стороны равны,то найдем одну сторону:
104/4 = 26 (см.) - длина стороны.
Что бы найти площадь,нам нужно найти вторую диагональ BD.
Рассмотрим треугольник BOС. ВС равно - 26 (см.),ОС равно половине диагонали АС - 10 (см.) (так как диагонали точкой пересечения делятся пополам),так как диагонали ромба перпендикулярны,то угол О- прямой,а значит треугольник ВОС - прямоугольный.Найдем ВО за теоремой Пифагора:
ВО =
Так как диагонали ромба делят его на 4 равных прямоугольных треугольника,то ВО=ОD и ВО+ОD=BD.
Диагональ BD = 24+24 = 48 (см.)
Теперь найдем площадь ромба:
S=
S=
ответ: 480