Question

498. Синус угла между образующей конуса, равной 100, и плоскостью основания равен 0,6. Найдите периметр соевого сечения конуса.
504.
Радиус основания конуса равен 2, а угол между образующей и плоскостью основания 60°. Найдите его объём.
P.s Дано, формула, решение.

Answer 1

1. Периметр соевого сечения конуса равен 360 ед.

2. Объем конуса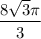 $\displaystyle \frac{8\sqrt{3}\pi }{3}$ ед.³

Объяснение:

Требуется найти:

1. Периметр соевого сечения конуса.

2. Объем конуса.

498.

Дано: Конус.

АК = 100; sin∠АКО = 0,6.

Найти: Р (КАМ)

1. Рассмотрим ΔКАО - прямоугольный.

Синус угла - отношение противолежащего катета к гипотенузе.

$\displaystyle sin\angle{AKO} = 0,6frac{AO}{AK}=0,6\\ \\AO = 0,6\cdot{AK} = 0,6\cdot100 = 60$

По теореме Пифагора:

КО² = АК² - АО²

КО² = 10000 - 3600 = 6400

КО = 80

⇒ КМ = 80 · 2 = 160

Р (КАМ) = АК + АМ + КМ = 100 + 100 + 160 = 360 (ед.)

504.

Дано: Конус;

r = СО = 2; ∠ВСО = 60°;

Найти: V конуса.

Объем конуса найдем по формуле:

$\displaystyle V=\frac{1}{3}\pi r^2h$, где r - радиус основания, h - высота конуса.

1. Рассмотрим ΔСВО - прямоугольный.

Тангенс угла - отношение противолежащего катета к прилежащему.

$\displaystyle tg\angle{BCO}=tg60^0=\frac{BO}{CO}=\sqrt{3} BO = 2\sqrt{3}$

2. Найдем объем:

$\displaystyle V=\frac{1}{3}\pi \cdot4\cdot2 \sqrt{3}=\frac{8\sqrt{3}\pi }{3}$ (ед.³)