
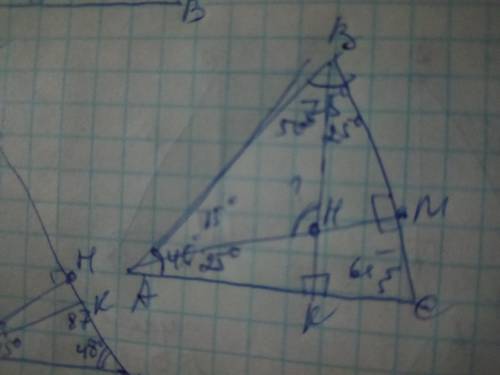
Зная, что ∠ВАС=40°, а угол АВС=75°, и сумма углов треугольника составляет 180°, найдём угол С.
Угол С=180-40-75=65°. Рассмотрим полученный ∆САМ. Он прямоугольный так как УГОЛ АМС=90°, найден угол С=65°, и так как сумма острых углов прямоугольного треугольника составляет 80°, то угол САМ=90-65=25°. Если угол САМ=25°, то угол ВАН=40-25=15°. Рассмотрим ∆СВК. Он также прямоугольный, так как угол ВКС=90°, угол С=65°, поэтому угол СВК=90-65=25°. Если угол СВК=25°, то угол АВН=75-25=50°
Теперь рассмотрим ∆АВН. В нём известны 2 угла: угол ВАН=15°, а угол АВН=50° и можно найти АНВ. Угол АНВ=180-50-15=115°
ОТВЕТ: угол АНВ=115°
1. 108 см²
2. АВ=ВС=10+2√5; АС=4√5 (см рисунок)
Объяснение:
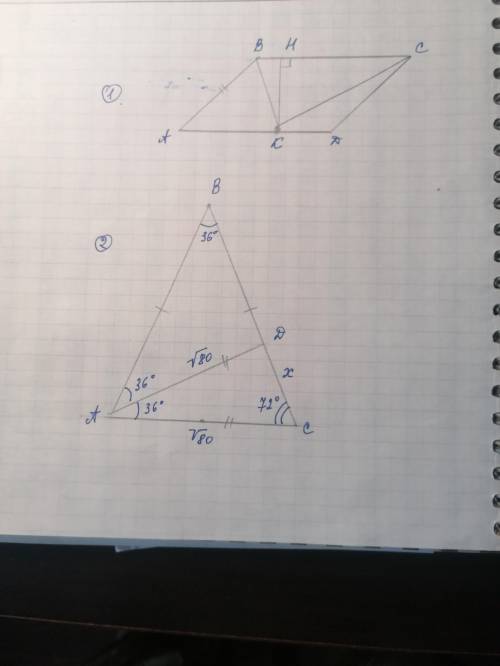
1.
У параллелограмма попарные стороны равны⇒АВ=СД=9 см, а АД=ВС
Биссектриса угла параллелограмма отсекает от него р/б Δ⇒
Биссектриса ∠В отсекла р/б Δ АВК ⇒АК=АВ=9 см
Биссектриса ∠С отсекла р/б Δ СДК ⇒КД=СД=9 см
АД=9+9=18 см
КH является высотой параллелограмма, т к точка К лежит на ВС. Расстоянием между параллельными прямыми называется расстояние от какой-нибудь точки одной прямой до другой прямой.
Можем посчитать площадь:
S=АД*КН=18*6=108 см²
2.
Обозначим Δ буквами АВС, где ∠В=36° (см рисунок) и АВ=ВС, и найдем два остальных угла р/б ΔАВС=(180-36)\2=72°
Биссектриса поделила ∠А пополам ⇒∠ВАД=∠ДАС=36°. Найдем ∠АДС=180-36-72=72°
Мы видим, что Δ САД подобен ΔАВС (по трем углам).
Выразим соотношение сторон: АС/ДС=ВС/АД
Возьмем СД за х, тогда АВ=ВС=√80+х:
√80/х=(√80+х)/√80⇒х(√80+х)=√80*√80=
х²+√х-80=0 Решим уравнение:
Дискриминант равен: (√80)²-4*1*(-80)=80+320=400=20²
Найдем корни:
***√80=√16*√5=4√5
X=(-√80+√20²)/2*1=(-√80+20)/2=(-4√5+20)/2=2(-2√5+10)/2=-2√5+10=10-2√5 - это ДС
Посчитаем все стороны ΔАВС:
АВ=ВС=4√5+(10-2√5)=4√5+10-2√5=10+2√5
АС=√80=4√5
Так угол прямоугольного треугольника равен 45°, то катеты равны,значит расстояние равно 10см