Объяснение:
D=2R=12см
α=90°
V- ?
радиус основания конуса
R=D/2=12/2=6 см
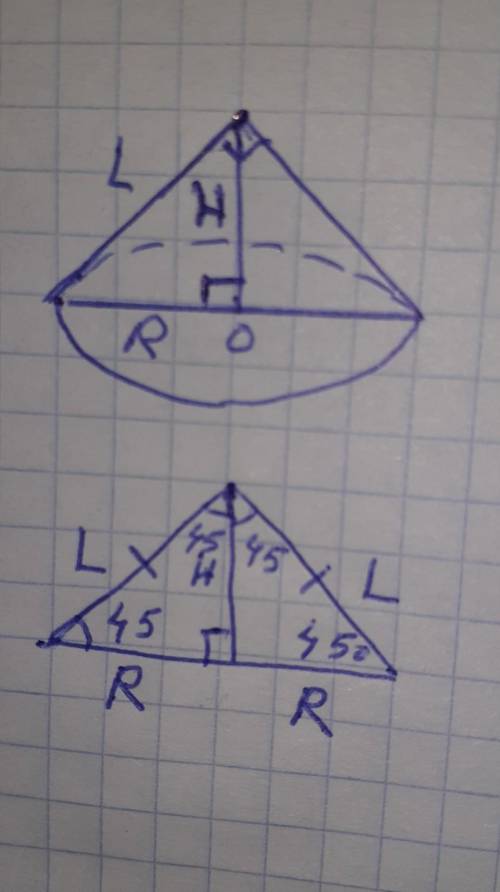
угол при вершине осевого сечения α=90° , то есть прямой угол. значит образующая конуса наклонена под углом 45° к плоскости основания и сечение выглядит как равнобедренный прямоугольный треугольник.
высота конуса равна радиусу основания конуса ,H=R=6см
так как вершина конуса перпендикулярно основанию конуса, и угол при вершине между высотой и образующей конуса 180°-90°-45°=45°
объем конуса
V=1/3 ×πR²×H=1/3 ×π×6²×6=72π см³
или V=72π=72×3,14=226,08 см³
Объяснение:
D=2R=12см
α=90°
V- ?
радиус основания конуса
R=D/2=12/2=6 см
угол при вершине осевого сечения α=90° , то есть прямой угол. значит образующая конуса наклонена под углом 45° к плоскости основания и сечение выглядит как равнобедренный прямоугольный треугольник.
высота конуса равна радиусу основания конуса ,H=R=6см
так как вершина конуса перпендикулярно основанию конуса, и угол при вершине между высотой и образующей конуса 180°-90°-45°=45°
объем конуса
V=1/3 ×πR²×H=1/3 ×π×6²×6=72π см³
или V=72π=72×3,14=226,08 см³

У нас дан ромб, а ромб - параллелограмм, значит, у него противоположные углы равны >> угол D= угол В=150 градусов. Вычислим углы А и С:
Угол А= угол С=180 - угол D=180 - угол B=30 градусов.
Проведем высоту DH к AB. Катет ДН равен половине гипотенузы, так как он лежит против угла в 30 градусов(угла А), следовательно, ДН=3см.
Проведем диагональ BD. Она разделит ромб на два равных треугольника(по трем сторонам, где диагональ - общая сторона). Значит, площади этих треугольников равны, а значит, площадь ромба будет равна удвоенной площади треугольника ABD. А площадь ABD мы можем найти, зная высоту и сторону, к которой эта сторона проведена.
S(ABD)=0,5*AB*DH=0,5*6см*3см=4,5 см^2
Теперь умножаем на два эту площадь и получаем площадь ромба, равная 9 см^2
ответ:9см^2