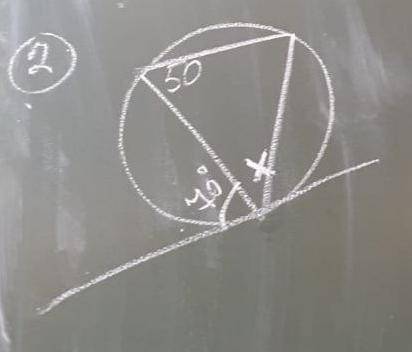
Задача 1
Решение(согласно моему рисунку)
1) Проведем высоту ВН.
2) Рассмотрим четырехугольник АВНД
Он будет параллелограммом, т.к. АВ || СД (как основания), а АД || ВН (т.к. высоты к одной стороне)
Тогда, т.к. АВНД - параллелограмм, АВ=ДН=6 см., АД=ВН (по св-ву параллелограмма)
3) Рассмотрим прямоугольный треугольника ВНС
НС=10 - 6=4 см.
Угол С=60° (по условию)
Тогда угол НВС=90° - 60°=30°.
В прямоугольном треугольнике против угла в 30° лежит катет, равный половине гипотенузы. Гипотенуза ВС=8 см. (это и будет большая боковая сторона)
ВС²=ВН² + НС² (теорема Пифагора)
ВН²=64 - 16
ВН²=48
ВН=4√3
4) ВН=АД=4√3, тогда АД=4√3 (это и будет меньшая боковая сторона)
ответ: АД=4√3 см., ВС=8 см.
Объяснение:
Смотри прикреплённый рисунок.
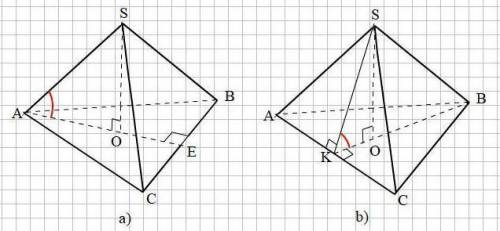
Пусть а = 8 см - ребро тетраэдра
a) В основании АВС проведём высоту АЕ ⊥ ВС. АЕ = 0,5а√3;
Опустим высоту SO на плоскость АВС.
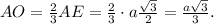
Угол между прямой SA и плоскостью АВС есть угол SAO
b) В основании АВС проведём высоту BK ⊥ AС. BK = 0,5а√3;
Опустим высоту SO на плоскость АВС.
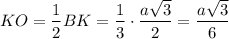
Проведём в грани SAC апофему SK = 0,5а√3
Угол между плоскостями SAC и АВС есть угол SKO между апофемой SK и высотой основания ВК как угол между двумя перпендикулярами, восставленными из точки К к линии пересечения АС плоскостей SAC и АВС
Поскольку тетраэдр правильный, то углы между любой боковой плоскостью и плоскостью основания равны между собой. И косинус между плоскостью SBC и плоскостью АВС равен 1/3.
60°
Объяснение:
Поставим в центр окружности точку О, и построим из неё радиусы. Построим касательные к окружности в вершинах треугольника.
1. В треугольнике АОВ угол ОАВ = 20°, т.к. по условию угол между хордой АВ и касательной А равне 70°, а угол между радиусом и касательной к нему всегода 90°
2. Треугольник АОВ равнобедренный, углы при основании 20°, угол при вершине
∠АОВ = 180 - 20 -20 = 140°
3. ∠АВС = 50° по условию, значит
∠ОВС = 50 - 20 = 30°
4. Треугольник ОВС равнобедренный, углы при основании 30°, угол при вершине
∠АОВ = 180 - 30 - 30 = 120°
5. Найдём угол при вершине равнобедренного треугольника АОС
∠АОС = 360 - 140 - 120 = 100°
6. Угол при основании ΔАОС
∠ОАС = (180 - 100)/2 = 40°
7. Добрались до финала :)
x = ∠ВАС = 20 + 40 = 60°