
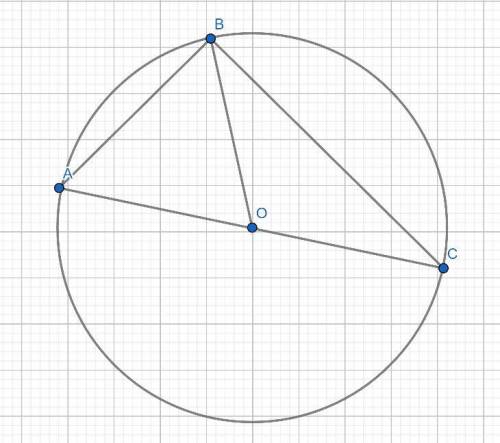
Дан прямоугольный ΔABC с прямым углом B. BO - медиана, проведенная из вершины прямого угла. Опишем около ΔABC окружность. Тогда гипотенуза AC будет являться диаметром окружности, так как вписанный угол ABC является прямым, то он опирается на диаметр окружности.
Медиана в треугольнике является отрезком, опущенным из вершины треугольника на середину противолежащей стороны. BO делит AC пополам. BO соединяет точку на окружности и центр окружности - тч.О, т.е. является радиусом окружности.
Отрезки BO = AO = OC - являются радиусами одной и той же окружности. ⇒ BO = AC/2.
ответ: tgB = 0,75 .
Объяснение:
ΔABC - прямокутний ; ∠С = 90° ; ВС = 4 см ; sinA = 0,8 ; tgB - ?
sinA = BC/AB ; AB = BC/sinA = 4/0,8 = 5 ( см ) . За Т. Піфагора
АС = √( АВ² - ВС² ) = √ ( 5² - 4² ) = √9 = 3 ( см ) ;
tgB = AC/BC = 3/4 = 0,75 ; tgB = 0,75 .