Угол 1 и противоположный ему угол равны,как вертикальные углы,значит на чертеже вместо вертикального угла мы поставим угол 1,тогда угол 1 и угол 2 будут называться односторонними и их сумма будет 180 градусов
<1+<2=180
Если эти углы соотносятся как 5:7,то мы их сейчас вычислим
5+7=12
Чему равна 1 часть?
180:12=15 градусов
<1=15•5=75 градусов
<2=15•7=105 градусов
Номер 2
Можно сказать так-угол 110 градусов и соседний с ним,который поделён на два равных угла,являются смежными,их сумма составляет 180 градусов
180-110=70 градусов
Этот угол по условию задачи поделён на 2 равных угла и один из них угол Х
<Х=70:2=35 градусов
Угол 70 градусов и угол У называются соответственными и равны между собой
<У=70 градусов
Объяснение:
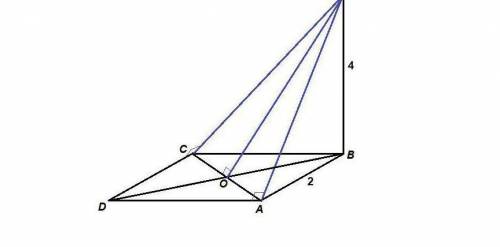
d(М, АВ) = d(M, BC) = 4 дм
d(M, AD) = d(M, СD) = 2√5 дм
d(M, BD) = 4 дм
d(M, AC) = 3√2 дм
Объяснение:
Расстояние от точки до прямой - длина перпендикуляра, проведенного из точки к этой прямой.
МВ - перпендикуляр к плоскости квадрата, а значит, и к любой прямой, лежащей в этой плоскости.
МВ⊥АВ, значит расстояние от точки М до прямой АВ
d(М, АВ) = МВ = 4 дм
МВ⊥ВС, значит
d(M, BC) = MB = 4 дм
МВ⊥BD, значит
d(M, BD) = MB = 4 дм
BA⊥AD как стороны квадрата,
ВА - проекция МА на плоскость, значит МА⊥AD по теореме о трех перпендикулярах, тогда
d(M, AD) = MA
Аналогично, ВС⊥CD как стороны квадрата, ВС - проекция МС на плоскость, значит МС⊥CD по теореме о трех перпендикулярах, тогда
d(M, СD) = MС
Если равны проекции наклонных, проведенных из одной точки, то равны и сами наклонные:
ВС = ВА (стороны квадрата), значит МС = МА.
Из прямоугольного треугольника АВМ по теореме Пифагора:
МА = √(АВ² + ВМ²) = √(4 + 16) = √20 = 2√5 дм
Итак,
d(M, AD) = d(M, СD) = 2√5 дм
Осталось найти расстояние от М до диагонали АС.
ВО⊥АС по свойству диагоналей квадрата,
ВО - проекция МО на плоскость квадрата, значит
МО⊥АС по теореме о трех перпендикулярах.
d(M, AC) = MO
BD = AB√2 =2√2 дм как диагональ квадрата,
BО = BD/2 = √2 дм (диагонали квадрата делятся точкой пересечения пополам)
Из прямоугольного треугольника МВО по теореме Пифагора:
МО = √(ВО² + ВМ²) = √(2 + 16) = √18 = 3√2 дм
d(M, AC) = 3√2 дм
Найдём гипотенузу по двум катетам:
ответ: A. √41см