Заполните пропуски в тексте так, чтобы получилось правильное построение. Задача. Постройте квадрат с центром в данной точке O так, чтобы середины двух его
a) противоположных; b) соседних сторон
принадлежали прямым ℓ1 и ℓ2, пересекающимся в точке X.
Решение. a) При
Выбрать
повороте относительно O на 60∘
повороте относительно O на 90∘
симметрии относительно O
симметрии относительно X
симметрии относительно ℓ1
симметрии относительно ℓ2
середина стороны квадрата, лежащая на ℓ1, переходит в середину, лежащую на ℓ2. Построив точку пересечения K прямой ℓ1 и образа ℓ2 при указанном движении, получим середину одной из сторон квадрата. Тогда сторона квадрата лежит на прямой m, проходящей через K
Выбрать
параллельно ℓ1
параллельно ℓ2
перпендикулярно ℓ1
перпендикулярно ℓ2
перпендикулярно OK
. Применив три раза к прямой m
Выбрать
поворот относительно O на 60∘
поворот относительно O на 90∘
симметрию относительно O
, получим прямые, содержащие остальные стороны квадрата. Точки их пересечения — это вершины квадрата.
b) При
Выбрать
повороте относительно O на 60∘
повороте относительно O на 90∘
симметрии относительно O
симметрии относительно X
симметрии относительно ℓ1
симметрии относительно ℓ2
середина стороны квадрата, лежащая на ℓ1, переходит в середину, лежащую на ℓ2. Построив точку пересечения K прямой ℓ1 и образа ℓ2 при указанном движении, получим середину одной из сторон квадрата. Дальнейшее решение аналогично пункту a).
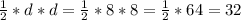 (дм²)
(дм²)
1. Многогранник - это геометрическое тело, ограниченное конечным числом плоских многоугольников, любые два смежных из которых не лежат в одной плоскости.
Сами многоугольники называют гранями многогранника, их стороны - ребрами многогранника, а их вершины - вершинами многогранника.
Диагональ многогранника - это отрезок, соединяющий две вершины многогранника, не лежащие в одной грани.
Примеры многогранников: пирамида, призма, параллелепипед, октаэдр, додекаэдр, икосаэдр.
2. Призма - это многогранник, у которого две грани - равные многоугольники с соответственно параллельными сторонами (называют основаниями), а остальные грани - параллелограммы (называют боковыми), у каждого из которых две стороны являются соответственными сторонами оснований.
Прямая призма - это призма, у которой все боковые грани - прямоугольники.
Правильная призма - это прямая призма, у которой в основании лежит правильный многоугольник.