Объяснение:
1)Если <С=90°, то АС и ВС - катеты, а АВ- гипотенуза. Косинус угла - это отношение прилежащего к углу катета к гипотенузе, используем эту формулу для нахождения гипотенузы АВ:
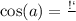
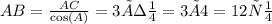
Теперь найдём ВС по теореме Пифагора:
ВС²=АВ²–АС²=12²–3²=144–9=135; ВС=√135=3√15см
ответ: АВ=12см, ВС=3√15см
2) синус - это отношение противолежащего от угла катета к гипотенузе поэтому
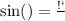
тогда АВ=
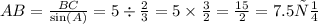
теперь найдём АС по теореме Пифагора:
АС²=АВ²–ВС²=7,5²–5²=56,25–25=31,25; АС=√31,25=
=2,5√5см
ответ: АВ=7,5см, АС=2,5√5см
3) тангенс - это отношение противолежащего от угла катета к прилежащему:
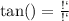
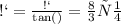
Теперь найдём АВ по теореме Пифагора:
АВ²=АС²+ВС²=
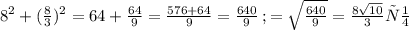
ответ: АВ=8√10/3см, ВС=8/3см
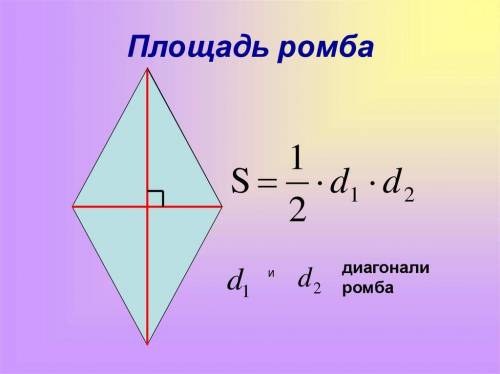
Периметр ромба P = 68 см
площадь ромба равна 240 см квадратных
Объяснение:
Ромб — это параллелограмм, у которого все стороны равны.
Периметр ромба P=4a = 4* 17 = 68 см
Если одна диагональ 30 см, то она образует с другой диагональю прямоугольный треугольник, с гипотенузой 17 см, и катетом 30/2 = 15 см.
второй катет равен корню из разности квадрата гипотенузы и квадрата известного катета = 8 см. Этот катет равен половине второй диагонали. Диагональ 2*8 = 16 см.
Следовательно площадь ромба равна (16*30)/2 = 240 см квадратных
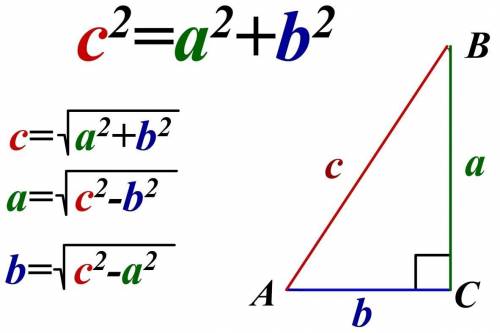
Объяснение:
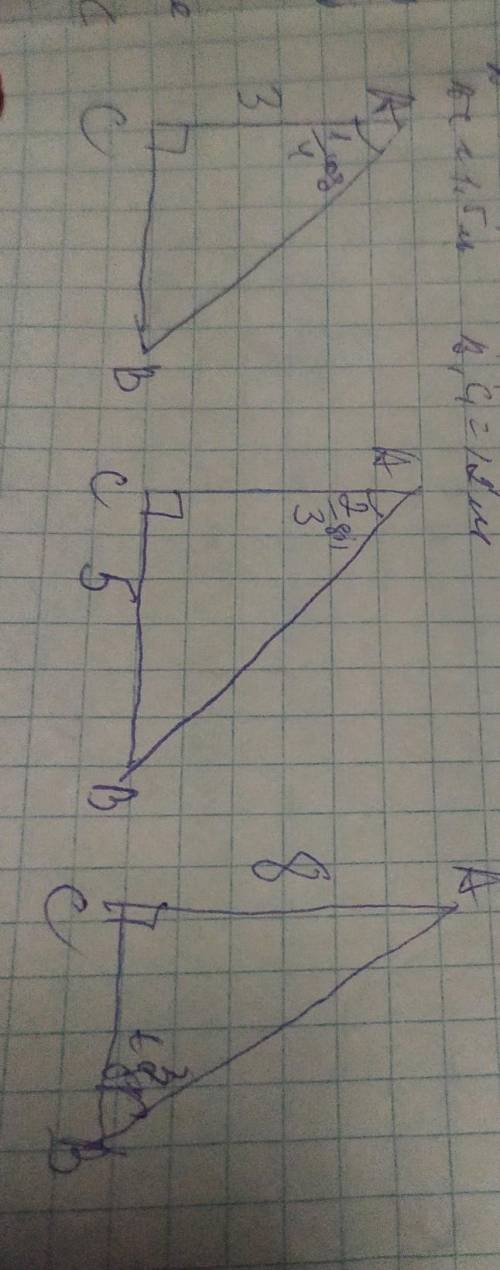
Проверяем треугольники с т. Пифагора.
а) 3²+6²=9+36=45, √45≈6,7 < 7 ⇒ треугольник остроугольный;
б) 7²+8²=49+64=113, √113≈10,6 > 10 ⇒ треугольник тупоугольный;
с) 6²+8²=36+64=100, √100=10 = 10 ⇒ треугольник прямоугольный.