Бисектриса прямого угла прямоугольного треугольника делит гіпотенузу на отрезки 40 см и 30 см. Найдите периметр треугольника.
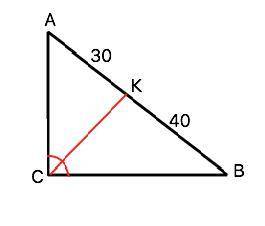
Обозначим треугольник АВС; СК - биссектриса. АК=30 см, ВК=40 см.
Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон. (свойство). АК:ВК=30:40=3:4. =>
АС:ВС=3:4. Из отношения катетов видно, что треугольник АВС - так называемый «египетский» с отношением сторон 3:4:5. .
Примем коэффициент отношения равным а.
Тогда АС=3а, ВС=4а, гипотенуза АВ=5а.
АВ=АВ+ВК=30+40=70 (см) => а=70:5=14(см).
Р=3а+4а+5а=12а
Р=12•14=168 (см)
1)а
2)по углам:а по сторонам:б
3)AB=AC+BC=8,5см
4)в (сумма острых углов в прямоугольном треугольнике равна 90°)
5)6+6+9=21см
6)б
2 часть
1)в равнобедренном треугольнике углы при основании равны, следовательно они равны 130°/2=65°
Сумма углов в треугольнике равна 180°. 180°-(65°+65°)=50°
ответ:65°,65°,50°
2) периметр ABD равен 17см, а высота равна 6, следовательно AB+AD=17-6=11 см. BD - медиана, следовательно AD=BD.
Рассмотрим треугольники ABD и CBD:
1)BD - общая сторона
2)AD=BD
3)ADB=CDB
Следовательно треугольники равны по двум сторонам и углу между ними.
Следовательно периметр треугольника АВС равен 11+11=22 см.
ответ: 22см.