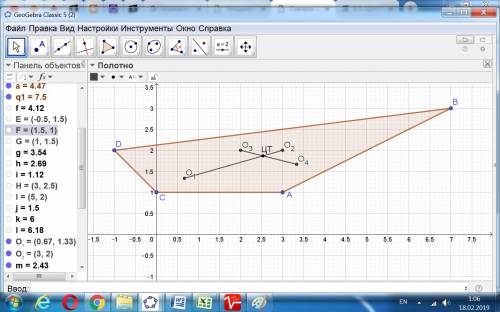
Сначала делим четырехугольник диагональю на два треугольника.
Находим центр тяжести каждого треугольника как точку пересечения его медиан. Центр тяжести четырехугольника лежит на прямой О1О2, соединяющей центры тяжести этих треугольников.
Затем делим четырёхугольник на 2 треугольника при другой диагонали и находим так же центры тяжести других треугольников. Соединяем их отрезком О3О4.
Искомый центр тяжести четырёхугольника лежит в точке ЦТ пересечения отрезков О1О2 и О3О4.
ABD x y BCD x y
O2 3 2 O3 2 2
ADC x y ABC x y
O1 0,6667 1,3333 O4 3,3333 1,6667
ЦТ = х у
2,533 1,8667
По определению в равнобедренном треугольнике боковые стороны равны.По свойствам равнобедренного треугольника известно, что высоты являются биссектрисами и медианами. Когда мы проведем высоты из вершин то получим маленькие треугольники они будут равны по боковым сторонам и двум углам, а в равных треугольниках соответственные элементы равны, следовательно высоты, которые являются сторонами равновеликих треугольников будут равны между собой.
Объяснение:
надеюсь прааильно если нет могу заново написать