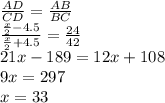В основании правильной пирамиды - правильный треугольник. Вершина S проецируется в центр О основания. Высота правильного треугольника СН= (√3/2)*а, где а - сторона треугольника. СН=13√3/2. В правильном треугольнике высота=медиана и делится центром в отношении 2:1, считая от вершины. => HO=(1/3)*CH, а СО=(2/3)*СН или СО=13√3/3, НО=13√3/6.
По Пифагору:
Боковое ребро пирамиды SC=√(CO²+SO²) = √(313/3).
Апофема (высота боковой грани) SH=√(НO²+SO²) = √(745/12).
Боковая поверхность Sбок = (1/2)*3*АВ*SH =(39/4)*(√(745/3).
ответ: б) AB = 18 см, AC = 6 см в) AC = 33 см
Объяснение:
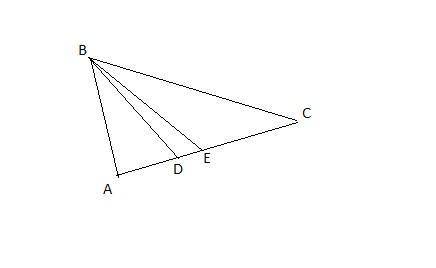
б) BC = BP + CP = 18 см
Обозначим две другие стороны Δ через x = AB и y = AC.
Из того, что периметр равен 42 получим:
x + y + 18 =42 ⇒ x + y = 24 (1)
Биссектриса делит противоположную сторону на отрезки пропорциональные сторонам ⇒
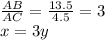
Подставим последнее равенство в (1) и получим:
4y = 24
y = 6
Тогда x = 18
в) Обозначим x = AC. Т.к. BE медиана, то AE = CE = x/2, AD = x/2 - 4.5, CD = x\2 +4.5
Биссектриса делит противоположную сторону на отрезки пропорциональные сторонам ⇒