
Каждое ребро правильной шестиугольной призмы равно а. Найдите площадь поверхности призмы.
---
Призма называется правильной, если ее боковые ребра перпендикулярны основаниям, а основания – правильные многоугольники.
Все ребра правильной призмы равны, ⇒
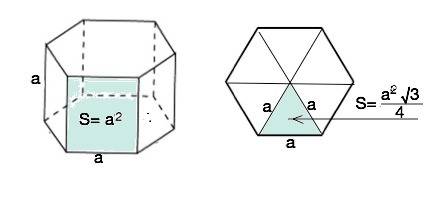
каждая из 6 боковых граней – квадрат, площадь которого S=a².
Ѕ(бок)=6а²
Основания правильной шестиугольной призмы - правильные шестиугольники, состоящие из 6 равных правильных треугольников.
Формула площади правильного треугольника S=(a²√3):4 ⇒
Ѕ (осн)•2=2•6•(a²√3):4=3а²√3
Площадь поверхности призмы равна сумме площадей: площади боковой поверхности и двух оснований.
S (призмы)= 6а²*+3•a²√3 или 3а²•(2+√3) ≈11,2а²
Объяснение:
(на фото рисунок и дано)
Доказательство:
1) Рассмотрим треугольники AMB и AMC:
они прямоугольные,т.к. СМ — высота(по усл),
АМ = ВМ(т.к. высота, проведённая к основанию в равнобедренный треугольнике, является медианой), СМ — общая, следовательно, треугольник АМВ = треугольнику АМС (по двум катетам)
ч.т.д.