Площа квадрата визначається по формулі: , де а - сторона квадрата.
Площа прямокутника визначається по формулі: , де a і b - сторони прямокутника.
===================================
Знаючи з умови, що сторона квадрата a = 12 см, можемо знайти й площу квадрата, й площу прямокутника (бо з умови площі фігур рівні).
см².
==================================
Також нам відома одна сторона прямокутника: a = 9 см. Знаючи площу S прямокутника ми підставляємо відому сторону у формулу площі прямокутника і шукаємо другу сторону:
Так как A внутри BCD, AB=AD, то BAD - тоже равнобедренный треугольник, и у него общее с BCD основание BD. Поставим точку K так, что BK=KD, тогда KC - медиана BCD, KA - медиана BAD. Докажем второй пункт. Как известно, высота равнобедренного треугольника совпадает с его медианой и биссектрисой и является его осью симметрии. Также, любые два равнобедренных треугольника, построенные на одном основании, обладают общей осью симметрии и, как следствие, общей высотой/медианой/биссектрисой. Тогда получаем, что KA⊂KC и все три точки лежат на KC. Это автоматически доказывает первый пункт, т.к. непонятные ∠ACB и ∠ACD превращаются в углы при биссектрисе ∠KCB=∠KCD, которые равны между собой.
16 см.
Объяснение:
Площа квадрата визначається по формулі: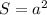 , де а - сторона квадрата.
, де а - сторона квадрата.
Площа прямокутника визначається по формулі: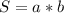 , де a і b - сторони прямокутника.
, де a і b - сторони прямокутника.
===================================
Знаючи з умови, що сторона квадрата a = 12 см, можемо знайти й площу квадрата, й площу прямокутника (бо з умови площі фігур рівні).
==================================
Також нам відома одна сторона прямокутника: a = 9 см. Знаючи площу S прямокутника ми підставляємо відому сторону у формулу площі прямокутника і шукаємо другу сторону: