Фронталь - это прямая, параллельная фронтальной плоскости : f║XOZ, значит, координата 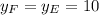 ⇒ F(15, 10, 40)
⇒ F(15, 10, 40)
Чтобы найти длину стороны квадрата, нужно найти расстояние от точки А до фронтали f.
1) Направляющий вектор фронтали f :
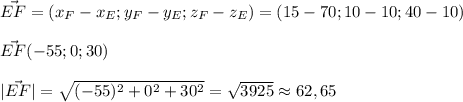
2) Вектор к точке на фронтали, проходящий через точку A
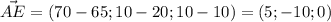
3) Векторное произведение
![[\vec {AE}\times \vec {EF}]=~\begin{vmatrix} \vec i ~~~~~\vec j ~~~~~\vec k\\ \ ~~5~~-10~~~0 \\ \ -55~~~0~~~30\\ \end{vmatrix}=-300\vec i-550\vec k-150\vec j\\](/tpl/images/0937/2964/b827d.png)
![[\vec {AE}\times \vec {EF}]=(-300; -150; -550)](/tpl/images/0937/2964/7a891.png)
![|[\vec {AE}\times \vec {EF}]|=\sqrt{(-300)^2+(-150)^2+(-550)^2}=\sqrt{415000}\approx 644,20](/tpl/images/0937/2964/a1c31.png)
4) Длина стороны квадрата - расстояние от точки А до фронтали
644,20 : 62,65 ≈ 10,28
5) Координаты точки В.
Точка В лежит на фронтали ⇒ 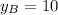
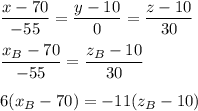
С другой стороны векторы 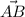 и
и 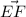 перпендикулярны, скалярное произведение равно нулю.
перпендикулярны, скалярное произведение равно нулю.
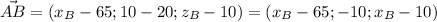
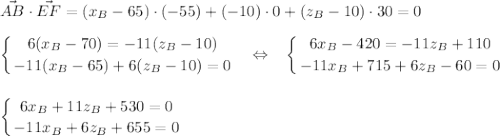
Решив систему, получаем координаты точки В (66,15; 10; 12,10)
Чтобы не искать координаты точек C и D, достаточно отложить от точки В длину стороны квадрата 10,28 на фронтальной плоскости. Так как ВС║XOZ, то проекция длины квадрата на фронтальную плоскость будет равна длине квадрата. Отложить можно в обе стороны. Возможно 2 варианта построения. В приложении дан чертёж для случая, когда точки C и D расположены к центру координат от точек A и B.
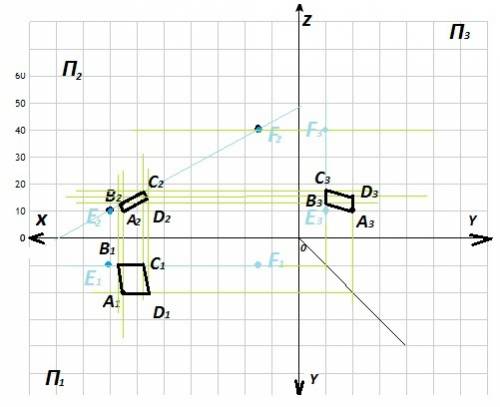
1) Треугольник ODF - равнобедренный, следовательно у него углы при основании равны.
Основанием является сторона DF, т.к. против неё лежит тупой угол Е=118 град., а в треугольнике не может быть больше одного тупого угла.
Следовательно углы D=F=(180-118):2=62:2=31 град.
2)Если DO - высота, то треугольник DOF - прямоугольный, угол DOF = 90град.
Угол OFD = 31 град.
Следовательно угол ODF=180-90-31=59 град.
ответ: 59 град