Находим векторы АВ и АС.
АВ = (-6; 0; -9), модуль равен √117 ≈ 10,81665383.
АС = (3; -4; -2), модуль равен √29 ≈ 5,385164807.
Площадь треугольника равна половине модуля векторного произведения векторов АВ и АС.
i j k| i j
-6 0 -9| -6 0
3 -4 -2| 3 -4 = 0i - 27j + 24k - 12j - 36i - 0k =
= -36i - 39j + 24k.
Модуль равен √((-36)² + (-39)² + 24²) = √3393 ≈ 58,24946352.
Площадь равна: S = (1/2)√3393 ≈ 29,12473176
.
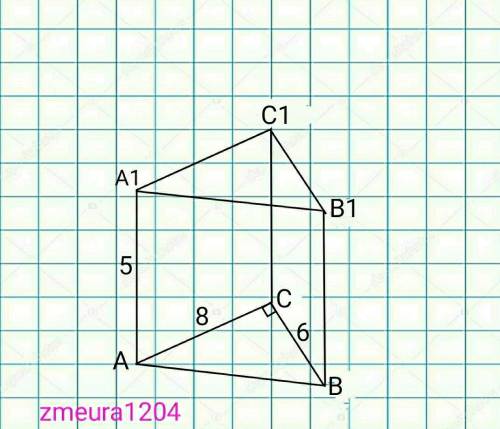
Площадь основания призмы - площадь треугольника АВС:
Sо=(1/2)*6*8=24см². Таких оснований два, S=48см².
Saa1b1b=6*4=24см².
Saa1c1c=8*4=32см².
ВС=√(6²+8²)=10см => Sbb1c1c=10*4=40см².
Sполн= 2*Sabc+Saa1b1b+Saa1c1c+Saa1c1c.
Sполн=48+24+32+40=144см².