Дан параллелограмм ABCD На продолжении диагонали АС за вершины А и С отмечены точки М и N соответственно так, что АМ = CN Докажите, что MBND –
Доказываешь, что два треугольник AMD и CNB:АМ = CN по условию,АВ=СВ, т.к. это стороны параллелограмма.По первому признаку равенства треугольников: AMD = CNBИз того же равенства треугольников получаешь, чтоПроверенные ответы содержат наджную, заслуживающую доверия информацию, оценнную командой экспертов. На «Знаниях» вы найдте миллионы ответов, правильность которых подтвердили активные участники сообщества, но Проверенные ответы — это лучшие из лучших.Диагональ ВD исходного параллелограмма АВСD осталась прежней, диагональACс каждой стороны увеличилась на одинаковую длину. Точка пересечения диагонали ВD и диагоналиМNосталась прежней и делит их, как и в исходном четырехугольнике, пополам.
Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то такой четырехугольник параллелограмм.
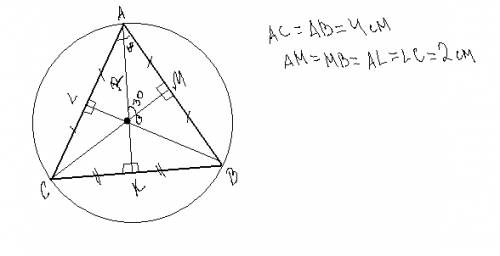
Центр описанной окружности треугольника - это точка пересечения серединных перпендикуляров. Исходя из этого можно сделать следующие вычисления:
Сначала найдем неизвестный угол равнобедренного треугольника: 180 - (30+30) = 120.
Затем проведем серединные перпендикуляры от каждой стороны треугольника и получим несколько прямоугольных треугольников, гипотенузой которых является расстояние от точки пересечения перпендикуляров до углов. Это расстояние есть радиус описанной окружности. Теперь воспользуемся чертежом. Найдем половину угла А: 120/2 = 60. Вычислим величину угла АОМ: 180 - (60+90) = 30.
Катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы. Катет АМ = 2см, следовательно гипотенуза, она же - радиус, равна 2*2 = 4см.
ответ: R=4см.
При гомотетии квадрат переходит в квадрат.