Объяснение:
1. АО = ОВ как радиусы => треугольник АОВ равнобедренный
угол А = 40
угол ВОС - центральный, ОАВ - вписанный. Значит, ВОС = 40*2 = 80
2. При построении получаем прямоугольный треугольник ДОС с гипотенузой ОС = 16 и углом О = 60. ОД - радиус - катет.
Второй острый угол = 90-60 = 30
ОД лежит напротив угла в 30, значит он равен половине гипотенузы. То есть ОД = 16/2 = 8
3. Рассматриваем треугольники МОК и РОN
Они равны по 1 признаку: ОМ=ОР, ОК=ОN как радиусы окружности, углы между ними (вокруг точки О) равны как вертикальные.
Значит, углы М, К, Р и N также равные => МК параллельно PN т.к. накрест лежащие углы равны.
Любой угол можно разделить на несколько равных с циркуля.
Есть тупой угол АВС. Ставим циркуль на его вершину - точку В, и, выбрав произвольный раствор, делаем засечки на каждой из сторон угла - это точки О и О1. Дальше ставим циркуль поочередно на каждую из этих точек и, не меняя раствора циркуля, делаем засечки в примерном центре угла. Точка пересечения засечек - О2. Проводим отрезок ВК через точку О2. ВК - это биссектриса угла АВС, т.е. мы получили два равных угла АВК и СВК. Всё то же самое проделываем с каждым из этих углов, и в результате получаем четыре равных угла.


Углы, образованные при пересечении двух параллельных прямых секущей, или равны, или в сумме составляют 180°. Следовательно, нам дано значение одного из смежных углов.
а) второй угол равен 180° - 150° =30°.
б) один из углов равен Х градусов, второй - Х+70 градусов. Их сумма равна 2Х+70=180° => X=55°. Тогда меньший угол = 55°, второй = 125°.
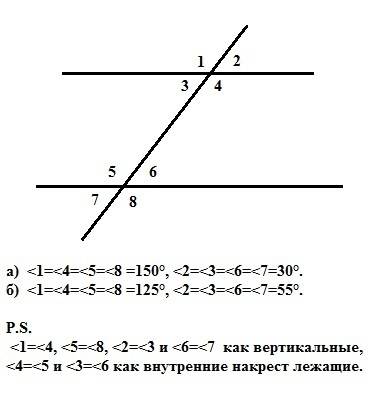
Или (см. рисунок): а) <1=<4=<5=<8 =150°, <2=<3=<6=<7=30°.
б) <1=<4=<5=<8 =125°, <2=<3=<6=<7=55°.
P.S.
<1=<4, <5=<8, <2=<3 и <6=<7 как вертикальные,
<4=<5 и <3=<6 как внутренние накрест лежащие.
1. Треугольник АВО - равнобедренный (радиусы ОА и ОВ равны). Значит угол ОАВ=40. Тогда угол ВОА = 180-40-40=100. Угол ВОС=180-100=80.
2. На фотографии
3. Углы МОК и PON равны (вертикальные). Треугольники МОК и PON равнобедренные (радиусы равны). Значит треугольники равны по 1 признаку. Тогда угол OKM равен углу OPN, а они накрест лежащие, значит MK||PN