V = 24√2·π.
Объяснение:
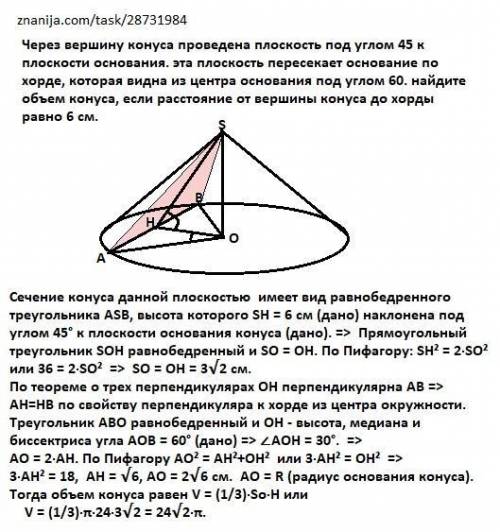
Сечение конуса данной плоскостью имеет вид равнобедренного треугольника АSВ, высота которого SН = 6 см (дано) наклонена под углом 45° к плоскости основания конуса (дано). => Прямоугольный треугольник SОН равнобедренный и SО = ОН. По Пифагору: SH² = 2·SO² или 36 = 2·SO² => SО = ОН = 3√2 см.
По теореме о трех перпендикулярах ОН перпендикулярна АВ => АН=НВ по свойству перпендикуляра к хорде из центра окружности. Треугольник АВО равнобедренный и ОН - высота, медиана и биссектриса угла АОВ = 60° (дано) => ∠AОН = 30°. => АО = 2·АН. По Пифагору А0² = АH²+OН² или З·АH² = OН² => З·АН² = 18, АН = √6, АО = 2√6 см. АО = R (радиус основания конуса). Тогда объем конуса равен V = (1/3)·Sо•Н или
V = (1/3)·π·24·3√2 = 24√2·π.
D = 13см - диагональ боковой грани призмы
R = 4√3 см - радиус описанной окружности
Известно, что в правильном треугольнике R = 2h/3, где h - высота треугольника. Тогда h = 3R/2 = 3 · 4√3 : 2 = 6√3(см)
Известно также соотношение междy стороной a правильного треугольника и его высотой h: h = 0.5a√3 . Откуда
а = 2h/√3 = 2 · 6√3 : √3 = 12(см)
Высота призмы Н находится по теореме Пифагора
H = √(D² - a²) = √(13² - 12²) = √25 = 5(cм)
ответ: 5см