Дано:
Окружность (О; r)
∠OBA = 30°
CA — касательная
Найти:
∠BAC — ?
1) Так как радиусы окружности равны, значит, две стороны треугольника ABO равны. ⇒ ΔABO равнобедренный (AO = OB).
У равнобедренного треугольника углы при основании равны, следовательно: ∠OBA = ∠OAB = 30°.
2) Касательная к окружности перпендикулярна радиусу, проведённому в точку касания, значит CA ⊥ OA. ∠OAC = 90°.
3) ∠BAC = ∠OAC - ∠OAB.
∠BAC = 90° - 30° = 60°.
ОТВЕТ: 60°
Быстрое решение (пояснения писать обязательно нужно):
1) ΔABO равнобедренный, так как радиусы окружности, составляющие стороны треугольника, равны (AO = OB). Следовательно, ∠OBA = ∠OAB = 30°.
По свойству касательной, CA ⊥ OA ⇒ ∠OAC = 90°. Значит:
2) ∠BAC = 90° - 30° = 60°
ОТВЕТ: 60°
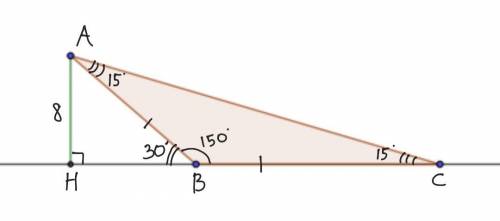
Дано: ΔABC - равнобедренный, АС - основание, АВ=ВС, ∠В=150°, АН - высота, АН = 8 е.д.
Найти: BC.
Решение.
Поскольку треугольник тупоугольный, а высота проведена из острого угла, то высота принадлежит продолжению противолежащей стороны.
Поэтому рисуем продолжение прямой ВС и высоту АН, проведённую к нему.
В ΔАНВ: ∠НВА = 180°-150°= 30° (как смежные).
АНВ - прямоугольный треугольник (АН ведь высота) с гипотенузой АВ.
В прямоугольном треугольнике, если острый угол равен 30°, то противолежащий этому углу катет равен половине гипотенузы.
АН=½АВ.
АВ= 2АН.
АН по условию 8, тогда АВ= 2×8=16.
ΔАВС - равнобедренный, АВ=ВС. Значит, ВС=16 е.д.
ответ: 16 е.д.
Доказательство:
1. По условию а⊥с, b⊥c, тогда по признаку аllb.
2. аllb, BC - секущая, тогда по свойству параллельных прямых ∠1 = ∠2 как внутренние накрест лежащие.
3. ∠1 = ∠3 = 90° : 2 = 45° (по условию), тогда и ∠3 = ∠2, ∆АВС равнобедренный по признаку, что и требовалось доказать.