Question

У правильній трикутній піраміді плоский кут при вершині дорівнює α . Визначити бічну поверхню піраміди, якщо радіус кола, описаного навколо бічної грані, дорівнює R.

Answer 1

Площадь боковой поверхности пирамиды равна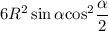 $6{R^2}\sin \alpha {\cos ^2}\displaystyle\frac{\alpha }{2}$

Объяснение:

Пусть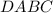 $DABC$ данная пирамида,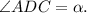 $\angle ADC = \alpha .$

Так как треугольник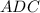 $ADC$ равнобедренный,

$\angle DAC = \angle DCA = \displaystyle\frac{{180^\circ - \alpha }}{2} = 90^\circ - \displaystyle\frac{\alpha }{2}.$

По теореме синусов для треугольника ADC

$\displaystyle\frac{{AC}}{{\sin \alpha }} = \displaystyle\frac{{AD}}{{\sin \left( {90^\circ - \displaystyle\frac{\alpha }{2}} \right)}} = 2R.$

Из первой и третьей частей равенства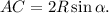 $AC = 2R\sin \alpha .$

По формуле приведения

$\sin \left( {90^\circ - \displaystyle\frac{\alpha }{2}} \right) = \cos \displaystyle\frac{\alpha }{2},$

откуда из второй и третьей частей равенства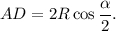 $AD = 2R\cos \displaystyle\frac{\alpha }{2}.$

Тогда площадь одной боковой грани

${S_1} = \displaystyle\frac{1}{2}AC \cdot AD\sin \angle DAC = \displaystyle\frac{1}{2} \cdot 2R\sin \alpha \cdot 2R\cos \displaystyle\frac{\alpha }{2} \cdot \cos \displaystyle\frac{\alpha }{2} = 2{R^2}\sin \alpha {\cos ^2}\displaystyle\frac{\alpha }{2},$

а площадь боковой поверхности

$S = 3{S_1} = 6{R^2}\sin \alpha {\cos ^2}\displaystyle\frac{\alpha }{2}.$

Answer 2

 Розв'язання завдання додаю