Правильная призма
- прямая - боковые грани перпендикулярны основанию
- в основании правильный многоугольник
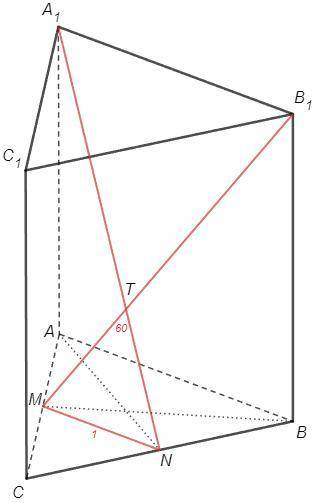
Проекциями отрезков A1N и B1M являются медианы AN и BM основания ABC. Следовательно, так же как и медианы равностороннего ABC, отрезки A1N и B1M равны и точкой пересечения T делятся 2:1.
MN=AB/2=1 (средняя линия)
MT=NT, ∠MTN=60° => △MTN - равносторонний (р/б с углом 60°)
MT=MN=1; B1M=3MT=3
BM=AB sin60° =√3
BB1 =√(B1M^2-BM^2) =√(9-3) =√6
V =S(ABC)BB1 =4 √3/4 *√6 =3√2
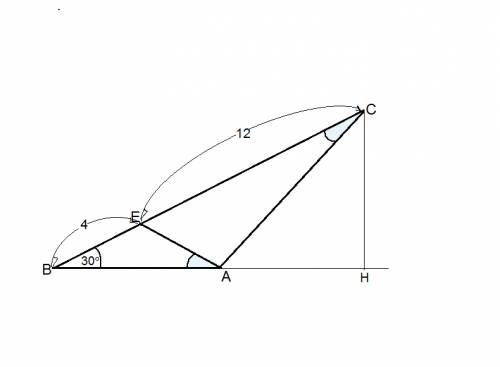
В треугольнике АВС найдем угол А. Угол А равен 90 - 60 = 30 град.
По свойству прямоугольного треугольника с углом 30 градусов катет, противолежащий этому углу в 2 раза меньше гипотенузы, т.е.ВС в 2 раза меньше АВ.
пусть ВС=х см, тогда АВ = 2х см. по теореме Пифагора составим уравнение:
24^2 + x^2 = (2x)^2 (24 в квадрате)
3x^2=576
x^2=192
x= корень из 192 = 8 корней из 3
Вс= 8 корней из 3
Тогда Ав = 2*8 корней из3 = 16 корней из3.
Значит ВД = 16 корней из 3
Теперь рассмотрим прямоугольный треугольник АСД. В нем АС=24 см, СД=24корня из 3. По теореме пифагора найдем гипотенуза АД:
АД^2=24^2+(24 корня из 3)^2= 576+576*3=576(1+3) = 576*4
Тогда АД=корень из (576*4)=24 *2=48(см0
ответ:48см
Объем призмы равен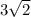
Объяснение:
(Рис. 1)
Тт.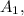
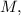
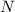 и
и 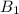 лежат в одной плоскости и, будучи соединены последовательно, образуют равнобокую трапецию (
лежат в одной плоскости и, будучи соединены последовательно, образуют равнобокую трапецию (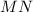 — средняя линия
— средняя линия 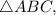 поэтому
поэтому 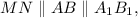
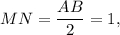
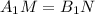 ).
).
Поэтому угол, о котором идет речь в условии задачи — это угол между диагоналями трапеции.
Далее возможны два варианта: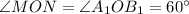 либо
либо 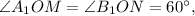 тогда
тогда 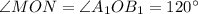 (см. рис. 2).
(см. рис. 2).
Решим задачу в общем виде (рис. 3). Пускай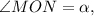
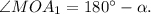 Продлим нижнее основание
Продлим нижнее основание 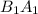 за точку
за точку 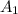 на длину верхнего основания:
на длину верхнего основания: 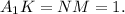 Тогда образовавшийся четырехугольник
Тогда образовавшийся четырехугольник 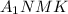 — параллелограмм,
— параллелограмм, 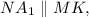
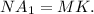 Значит
Значит 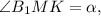 а
а
По теореме синусов
используя формулу приведения и формулу синуса двойного угла найдем длину диагонали:
Треугольники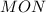 и
и 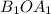 подобны,
подобны, 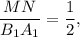 значит и
значит и 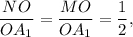 отсюда
отсюда
По теореме косинусов для треугольника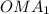
откуда
Тогда если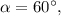
Если же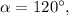 тогда
тогда
Теперь возвращаясь к призме, можем вычислить ее высоту. В прямоугольном треугольнике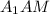 по теореме Пифагора:
по теореме Пифагора:
если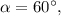
если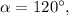
(при таком значении угла не складывается пространственная фигура — ее высота равна 0, следовательно, случай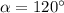 — посторонний).
— посторонний).
Площадь основания призмы вычислим по формуле площади равностороннего треугольника
Окончательно, объем призмы: