Свойство --- это характеристика известного объекта
(например, если дан ромб, то из этого следует,
что его диагонали взаимно перпендикулярны)))
а признак --- это характеристика неизвестного объекта, т.е.
необходимо определить что это за объект (по признакам)))
т.е. если сказано, что диагонали 4-угольника взаимно перпендикулярны,
то из этого не следует, что это ромб (это НЕ признак)))
если стороны 4-угольника равны, то точно ничего утверждать нельзя
--- может быть это ромб, а может быть это квадрат --- это НЕ признак))
а вот если известно, что это квадрат,
то точно у него стороны равны (это свойство)))
если известно, что это ромб,
то точно у него стороны равны (это свойство)))
если диагонали 4-угольника точкой пересечения делятся пополам,
то это точно параллелограмм (это ПРИЗНАК)))
это может быть и прямоугольник, это может быть и ромб
(они же все являются параллелограммами)))
дан треугольник (какой-то, не известно какой),
но про него известно, что две стороны у него равны (это ПРИЗНАК)
---вывод: это точно равнобедренный треугольник
дан равнобедренный треугольник (известно какой)
---вывод: у него две стороны точно равны (это СВОЙСТВО)
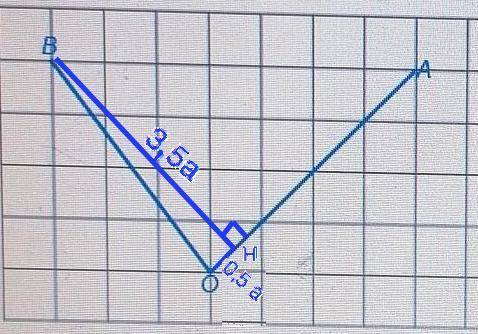
Найдите тангенс угла АОВ. сторона одной клетки равна 1. Запишите ответ в виде целого числа, обыкновенной или смешанной дроби.
ответ: 7
Объяснение.
Клетки на рисунке - квадратные. Следовательно, прямые, проведенные через их противоположные вершины, - их диагонали - пересекутся под прямым углом.
Проведем из В прямую по диагоналям соседних клеток к стороне ОА данного угла. Т.к. прямая ОА проходит также по диагонали клеток с общей вершиной, ВН перпендикулярен ОА. Треугольник ВОН - прямоугольный.
Примем диагональ клетки равной а. Тогда катет ОН=0,5а ( половина диагонали клетки), и ВН=3,5а.
Тангенс - отношение катета, противолежащего углу, к катету прилежащему.
tg AOB=tg НОВ=BH/OH=3.5/0.5=7
Відповідь:
Існує шість відрізків.
Пояснення:
Існує чотири точки А, В, С та D. Точки А, В та С лежать на одній прямій, а точка D не лежить на цій прямій ( дивись малюнок ).
Існують наступні відрізки з кінцями в точках А, В, С, D:
1) АВ;
2) ВС;
3) АС;
4) АD;
5) ВD;
6) СD.