5
Объяснение:
Так как острые углы трапеции 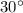 и
и 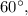 продлим ее боковые стороны до пересечения в точке
продлим ее боковые стороны до пересечения в точке 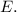 Тогда образовавшийся треугольник
Тогда образовавшийся треугольник 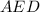 прямоугольный.
прямоугольный.
Его катет 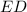 лежит напротив угла
лежит напротив угла 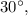 а значит равен половине гипотенузы:
а значит равен половине гипотенузы:
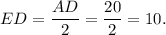
Треугольники 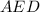 и
и 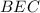 подобны с коэффициентом
подобны с коэффициентом
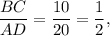
значит и боковая сторона 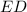 делится в том же отношении. То есть
делится в том же отношении. То есть
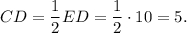
51 см или 57 см.
Объяснение:
Треугольник равнобедренный, а значит какие-то две стороны равны. Либо две стороны равны 15 см, либо две стороны равны 21 см.
Но существует неравенство треугольника, из которого следует, что одна из сторон обязана быть меньше, чем сумма двух других.
То есть в треугольнике АВС: АС < АВ+ВС; АВ < АС+ВС; ВС < АВ+АС
Проверим, какой равнобедренный треугольник с представленными сторонами может существовать:
Допустим АВ = 15 см, АС = 21 см, а ВС = 15 см.
Тогда АВ < АС+ВС (15 < 21+15 - верно), АС < АВ+ВС (21 < 15+15 - верно),
ВС < АВ+АС (15 < 15+21 - верно)
Такой треугольник может существовать.
Проверим второй вариант:
АВ = 15 см, АС = 21 см, а ВС = 21 см.
Тогда АВ < АС+ВС (15 < 21+21 - верно), АС < АВ+ВС (21 < 15+21 - верно),
ВС < АВ+АС (21 < 15+21 - верно)
И такой треугольник может существовать.
Ну а теперь найдем два варианта периметра этого треугольника (периметр - это сумма всех его сторон).
Периметр 1: 15см+21см+15см = 51см.
Периметр 2: 15+21см+21см = 57 см.
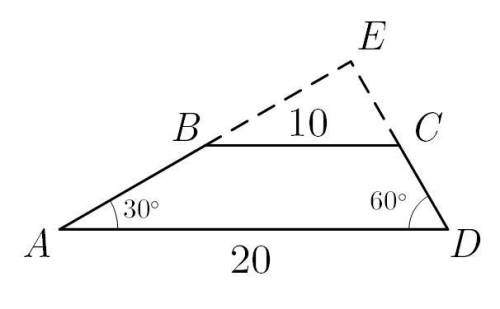
CD=5см
Объяснение:
Опустим высоты ВЕ и CF из вершин B и C на основу AD. BE⟂AD, CF⟂AD. BE=CF=h.
EBCF - прямоугольник, поэтому EF=BC=10 см.
Следовательно AE+FD=AD-BC=20-10=10см
Пусть FD=x, тогда AE =10-x.
1) △ABE(∠E=90°)
h=BE=AE•tg 30°=(10-x)•(√3/3)
2)△CDF(∠F=90°)
h=FC=x•tg 60° = √3•x
BE=FC
Обе части равенства умножим на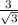 :
:
10-х=3х
4х=10
х=5/2
FD=5/2
Катет FD лежит напротив угла в 30°, поэтому он равен половине гипотенузы CD.CD=2•FD=2•(5/2)=5см