Пусть основания ВС и AD. Обозначим точку пересечения диагоналей - точку О. Проведем высоту через точку пересечения диагоналей. Высота делит основания равнобедренной трапеции пополам. Пусть отрезок высоты в треугольнике ВОС равен х, а отрезок высоты в треугольнике AOD равен (h-x). BC/2=x·tg((180°-α)/2) AD/2=(h-x)· tg((180°-α)/2)
Дан квадрат АВС1Д1. О1О2 - ось цилиндра. АВ⊥О1О2. Диагонали квадрата пересекаются наоси цилиндра в точке О. Через точку О проведём отрезок РЕ║АД1. ∠О2ОЕ=α. Сторона квадрата равна а. АЕ=ЕВ=а/2. Построим плоскость перпендикулярно оси О1О2, проходящую через сторону АВ. Проекция квадрата АВС1Д1 на эту плоскость будет прямоугольник АВСД. Диагонали прямоугольника АВСД пересекаются на оси цилиндра в точке М. Половина диагонали этого прямоугольника и есть радиус цилиндра. АМ=R. В тр-ке ЕОМ ЕМ=ОЕ·sinα=a·sinα/2 (ОЕ=РЕ/2=а/2). В тр-ке АМЕ АМ²=АЕ²+ЕМ²=(а²/4)+(а²sin²α/4)=2a²sin²α/4. AM=a√2·sinα/2 ответ: радиус цилиндра
Объяснение:
Выполним дополнительное построение: через основание высоты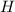
проведем прямую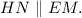 
Тогда в треугольнике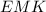
отрезок 
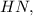проходящий через точку 
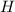— середину стороны 
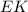параллельно основанию 
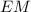— средняя линия. Значит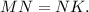 
А в треугольнике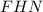
отрезок 
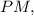проходящий через середину стороны 
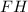параллельно основанию 
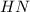— средняя линия. Значит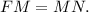 
Таким образом, точк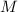и
и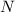 
разбивают сторону 
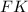на три равные части. Значит 