Один из углов, образовавшихся при пересечении двух прямых, равен 450. Найди остальные углы.

👇

Ответ:

Леля24579

14.12.2022

$45^\circ ,\,\,135^\circ ,\,\,135^\circ$

Объяснение:

При пересечении двух прямых образуются четыре угла, по два вертикальных, каждые два из которых смежные, т. е. их сумма равна $180^\circ .$

Если один из углов равен $45^\circ ,$ то смежный ему $180^\circ - 45^\circ = 135^\circ .$

Значит прямые разбили плоскость на углы $45^\circ ,\,\,45^\circ ,\,\,135^\circ ,\,\,135^\circ .$

4,4(99 оценок)

Открыть все ответы

Ответ:

katyunyakim123

14.12.2022

Медианы, биссектрисы и высоты треугольника.

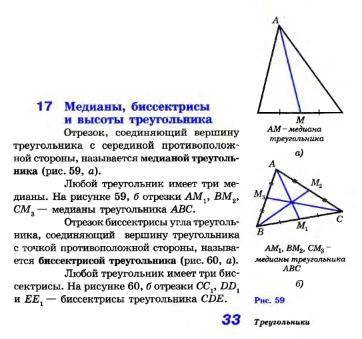
Медиана треугольника - отрезок, соединяющий вершину треугольника с серединой противоположной стороны. (рис, 59 а)

Биссектриса треугольника - отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. (рис. 60 а)

Высота треугольника - перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону. (рис. 61)

Любой треугольник имеет:

· три медианы (рис. 59 б)

· три биссектрисы (рис. 60 б)

· три высоты (рис. 62 а, б, в)

Свойства:

- в любом треугольнике медианы пересекаются в одной точке.

- в любом треугольнике биссектрисы пересекаются в одной точке.

- в любом треугольнике высоты или их продолжения пересекаются в одной точке.

Конспект на тему медианы,биссектрисы и высоты треугольника

4,5(88 оценок)

Ответ:

Gay1122

14.12.2022

Точка К, из которой будет виден отрезок МN под наибольшим углом, будет находиться на общей окружности с точками М и N. При этом OK для неё является касательной.
По свойству касательной и секущей ОК²=ОМ·ОN.
Пусть ОМ=х, тогда ОN=OM+MN=x+6,
4²=x(х+6),
х²+6х-4=0,
х1=-8, отрицательное значение не подходит,
х2=2.
ON=2+6=8 дм - это ответ.

Теперь докажем, что отрезок MN виден из точки К под большим углом.
Пусть радиус окружности около тр-ка КMN равен r.
На стороне ОК в любом месте возьмём точку Р и опишем окружность около тр-ка РMN, радиусом R. ОР для неё является секущей, а для окружности, радиусом r - касательной, значит R>r.
Формула хорды: l=2R·sin(x/2), где х - градусная мера хорды.
∠MKN=α, ∠MPN=β.
Обратим внимание, что углы α и β - это половина градусной меры хорды.
MN=2R·sinβ ⇒ sinβ=MN/2R.
MN=2r·sinα ⇒ sinα=MN/2r.
Сравним синусы, предположив, что они равны.
MN/2R=MN/2r.
1/R=1/r, но R>r, значит 1/R<1/r, значит sinβ<sinα.
Так как градусная мера хорды не может быть больше 180°, значит в формуле хорды 0°<α<90°, 0°<β<90°.
В этом диапазоне синус угла тем больше, чем больше его градусная мера,
значит α>β.
Доказано.
Решить на одной из сторон острого угла с вершиной о отмечены точки м и n ( м лежит между о и n). на