Так как отрезки РР₁ и ММ₁ перпендикулярны плоскости а, то указанные отрезки лежат на одной плоскости, а точка Р₁ лежит на отрезке КМ₁.
Рассмотрим ∆КРР₁ и ∆КММ₁.
Угол МКМ₁ – общий;
Угол КР₁Р=угол КМ₁М (оба прямые, так как РР₁ и ММ₁ перпендикулярны КМ₁)
Следовательно ∆КРР₁~∆КММ₁ по двум углам.
Пусть КР=n, тогда РМ=2n (из отношения КР:РМ=1:2), следовательно КМ=KP+PM=n+2n=3n.
Отношение двух любых сторон одного треугольника, равно отношению двух соответствующих сторон треугольника, подобного первому. Тогда:
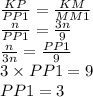
ответ: 3 см
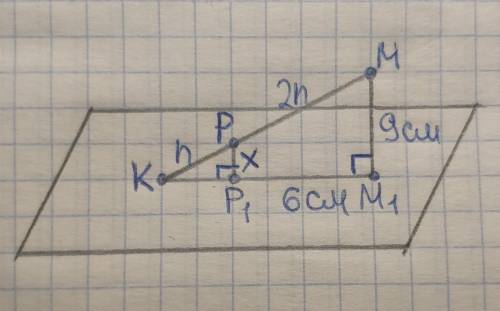

Доказано, что луч РА проходит через середину стороны MN.
Объяснение:
В середине равнобедренного треугольника MNP (PM=PN) взята точка А так, что ∠AMN = ∠ANM. Докажите что луч РА проходит через середину стороны MN.
Дано: ΔMNP - равнобедренный (PM=PN);
А ∈ (MNP)
∠AMN = ∠ANM
Доказать: МК = KN
Доказательство:
1. Рассмотрим ΔMAN.
∠AMN = ∠ANM (условие)
Если в треугольнике два угла равны, то этот треугольник равнобедренный.⇒ MA = AN
2. Рассмотрим ΔМРА и ΔAPN.
MA = AN (п.1)
PM = PN (условие)
РА - общая.
⇒ ΔМРА = ΔAPN (по трем сторонам, 3 признак)
⇒ ∠МРА = ∠АРN (соответственные элементы)
3. Рассмотрим ΔМNP - равнобедренный.
РК - биссектриса (п.2)
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой.⇒ МК = КN.
#SPJ1