Построим координатный параллелепипед точки А. Отметим на оси х — Ах(1;0;0); у — Ау(0;2;0); z — Аz (0;0;3).
Затем из точки Ах проведем две прямые, параллельную оси у и оси z, из точки Ау — прямые параллельные оси x и оси z; из Аz — параллельные оси х и оси у.
При пересечении прямых получаются точки Аху, Ауz, Ахz. Тогда
AxAxy = 2; AxAxz = 3; AyAxy = 1; AyAyz = 3; AzAxz = 1; AzAyz = 2;
Перпендикулярами на координатные оси будут отрезки ААz ААу; АAх на координатные плоскости αху, Ауz АХz. Получаем что основания перпендикуляров: Аху(1;2;0), Аyz(0;2;3), Аxz(1;0;3).ответ:
Объяснение:
Объяснение:
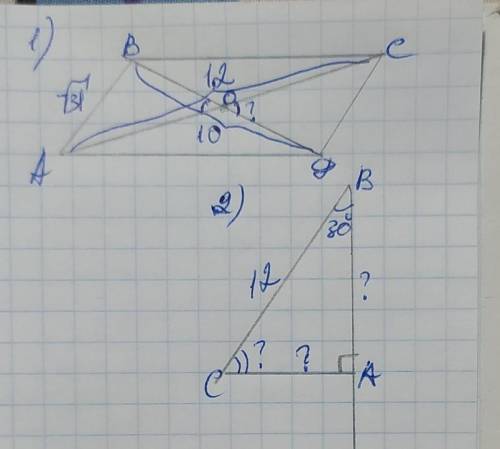
Обозначим пересечение диагоналей точкой О. Диагонали параллелограмма точкой пересечения делятся пополам, поэтому АО=СО=12÷2=6(ед), а ВО=ДО=10÷2=5(ед).
Для нахождения ∠АОВ воспользуемся теоремой косинусов:
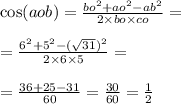
cos(1/2)=60°
ОТВЕТ: ∠АОВ=60°
2) Сумма острых углов прямоугольного треугольника равна 90°, поэтому
∠С=90–∠В=90–30=60°
∠С=60°
Катет АС лежит напротив угла 30°, поэтому он равен половине гипотенузы ВС:
АС=ВС÷2=12÷2=6(ед)
По теореме Пифагора:
АВ²=ВС²–АС²=12²–6²=144–36=108
АВ=√108=6√3(ед)
ОТВЕТ: АС=6(ед); АВ=6√3(ед); ∠С=60°
Відповідь:
Щоб знайти точку М (x, y, z), яка рівновіддалена від точок A(-3, 2, 4) і B(2, 1, -3) на осі ординат, можемо скористатися властивістю рівновіддаленої точки.
Оскільки точка М рівновіддалена від точок A і B, значить, відстань від М до A дорівнює відстані від М до B.
Використовуючи формулу відстані між двома точками:
d = √((x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²),
де (x₁, y₁, z₁) та (x₂, y₂, z₂) є координатами точок, можемо записати рівняння відстаней:
√((x - (-3))² + (y - 2)² + (z - 4)²) = √((x - 2)² + (y - 1)² + (z - (-3))²).
Спрощуючи це рівняння, ми отримуємо:
(x + 3)² + (y - 2)² + (z - 4)² = (x - 2)² + (y - 1)² + (z + 3)².
Розкриваємо квадрати:
x² + 6x + 9 + y² - 4y + 4 + z² - 8z + 16 = x² - 4x + 4 + y² - 2y + 1 + z² + 6z + 9.
Скасовуємо подібні доданки:
6x - 4x + 9 - 4 + 6z - 8z + 16 = 4 - 1 + 9.
2x - 2z + 25 = 12.
2x - 2z = -13.
x - z = -13/2.
Отже, вираз x - z = -13/2 визначає рівновіддалену від осі ординат точку М (x, y, z) від точок A(-3, 2, 4) і B(2, 1, -3).
Пояснення: