Геометрия как систематическая наука появилась в Древней Греции, её аксиоматические построения описаны в «Началах» Евклида. Евклидова геометрия занималась изучением простейших фигур на плоскости и в пространстве, вычислением их площади и объёма. Осноположником геометрии можно считать Евклида. В начале XX века великий французский архитектор Ле Корбюзье сказал: «Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг – геометрия». В развитии Геометрия можно указать четыре основных периода, переходы между которыми обозначали качественное изменение Геометрии.
Первый — период зарождения Геометрии как математической науки — протекал в Древнем Египте, Вавилоне и Греции примерно до 5 в. до н. э. Первичные геометрические сведения появляются на самых ранних ступенях развития общества. Зачатками науки следует считать установление первых общих закономерностей, в данном случае — зависимостей между геометрическими величинами. Этот момент не может быть датирован. Самое раннее сочинение, содержащее зачатки Геометрия, дошло до нас из Древнего Египта и относится примерно к 17 в. до н. э., но и оно, несомненно, не первое. Геометрические сведения того периода были немногочисленны и сводились прежде всего к вычислению некоторых площадей и объёмов. Они излагались в виде правил, по-видимому, в большой мере эмпирического происхождения, логические же доказательства были, вероятно, ещё очень примитивными. Геометрия, по свидетельству греческих историков, была перенесена в Грецию из Египта в 7 в. до н. э. Здесь на протяжении нескольких поколений она складывалась в стройную систему. Процесс этот происходил путём накопления новых геометрических знаний, выяснения связей между разными геометрическими фактами, выработки приёмов доказательств и, наконец, формирования понятий о фигуре, о геометрическом предложении и о доказательстве.Геоме́трия (от др. ... γεωμετρία, от γῆ — земля и μετρέω — измеряю) — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения. Геометрия как систематическая наука появилась в Древней Греции, её аксиоматические построения описаны в «Началах» Евклида.
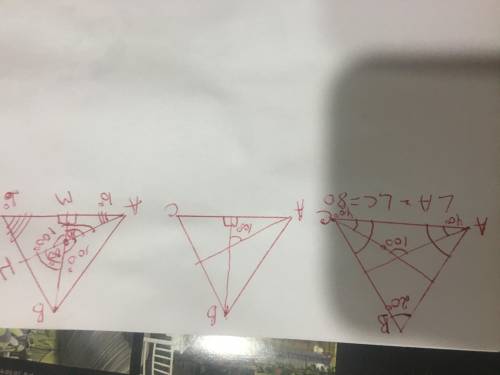
ответ:Бисмектрисы проведены из углов при основании и образуют при пересечении угол сто,тогда углы при основании образовавшегося треугольника будут по 40 градусов,т к углы при основании равнобедренных треугольников равны между собой,а биссектрисы поделят эти углы на 4 равных угла
А углы при основании равнобедренного треугольника АВС будут равны по 80 градусов,а угол при вершине
180-80•2=180-160=20 градусов
Так как в задаче не указано-из какого именно угла проведены две биссектрисы,то предположим второй вариант-одна биссектриса проведена из вершины треугольника,а вторая из угла при основании равнобедренного треугольника,если смотреть на чертёж 2 и угол находится именно там,то Задача не имеет решения,т к сумма всех углов треугольника равна 180 градусов,а в данном треугольнике биссектриса является еще и высотой ,т е перпендикуляром,образует с основанием два угла по 90 градусов,и получается сумма двух углов 190,чего не может быть никогда
Третий вариант-угол 100 АОВ,тогда
<АОВ=<МОН=100 градусов,как вертикальные,тогда
<АОМ<ВОН =80 градусов,как вертикальные
В треугольнике АОМ два угла-80 и 90 градусов,третий угол
<ОАМ=180-(90+80)=10 градусов,тогда <А треугольника АВС равен
<А=10•2=20 градусов,т к биссектриса поделила его на два равных угла
<А=<С=20 градусов,т к это углы при основании равнобедренного треугольника
Тогда угол при вершине равен
180-20•2=140 градусов
Объяснение:
Для знаходження площі трапеції можна скористатися наступною формулою:
Площа трапеції = ((a + b) * h) / 2,
де a і b - основи трапеції, h - висота трапеції.
У вашому випадку, основи трапеції дорівнюють 16 см і 4 см, а висота - 5 см. Підставляючи ці значення в формулу, ми отримуємо:
Площа трапеції = ((16 + 4) * 5) / 2 = (20 * 5) / 2 = 100 / 2 = 50 см².
Отже, площа цієї трапеції дорівнює 50 квадратним сантиметрам.
Объяснение: