ответ: 1) меньшие по 48°, большие по 132°.
2) меньшие по 40°, большие по 140°
Объяснение: При пересечении двух параллельных прямых секущей образуется пары равных углов:
соответственные (2 и 6, 1 и 5, 3 и 7, 4 и 8).
накрестлежащие: (3 и 5, 4 и 6 - внутренние ), (2 и 8, 1 и 7 - внешние). кроме того, равны и пары вертикальных углов.
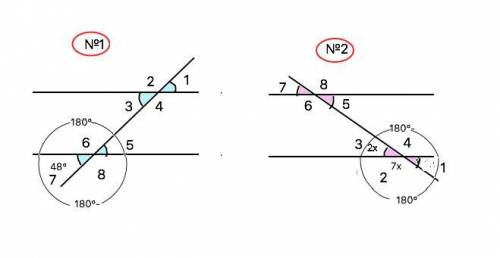
1) Как известно, сумма смежных углов равна 180°. Поэтому углы, смежные углу, равному 48°, равны 180°-48°=132°
На рисунке 1 все мéньшие углы, окрашенные голубым, равны 48°. все бóльшие - 132°
2) На рисунке 2 смежные углы 2 и 3 относятся как 2:7. Т.е. развернутый угол делится на 2+7=9 частей. Каждая часть равна 180°:9=20°. Поэтому все мéньшие углы равны 2•20°=40°, бóльшие 7•20°=140°.
Для розв'язання цієї задачі скористаємося властивостями трапеції та пропорціями.
Позначимо основи трапеції як AB і CD, а точку перетину діагоналей як M. Також позначимо довжину АМ як x, тоді довжину МС буде 2x (так як пропорція АМ:МС = 4:7).
За властивістю середньої лінії трапеції, довжина основ дорівнює сумі довжин діагоналей, поділеній на 2. Тобто:
AB + CD = 2 * середня лінія
AB + CD = 2 * 44 см
AB + CD = 88 см (1)
За умовою, пропорція АМ:МС = 4:7. Це означає, що:
AM/MS = 4/7
x / 2x = 4/7
Перекреслимо рівність, ми отримаємо:
7x = 4 * 2x
7x = 8x
x = 0
Це означає, що точка М збігається з точкою С, і діагональ МС збігається з основою CD. Таким чином, ми отримуємо:
AB + CD = 88 см (1)
AB + CD = 88 см
Тому, щоб знайти основи трапеції, ми повинні знайти значення, яке задовольняє рівняння (1). Оскільки в цьому випадку ми не маємо додаткових відомостей, неможливо однозначно визначити значення основ трапеції.