Так как отрезки РР₁ и ММ₁ перпендикулярны плоскости а, то указанные отрезки лежат на одной плоскости, а точка Р₁ лежит на отрезке КМ₁.
Рассмотрим ∆КРР₁ и ∆КММ₁.
Угол МКМ₁ – общий;
Угол КР₁Р=угол КМ₁М (оба прямые, так как РР₁ и ММ₁ перпендикулярны КМ₁)
Следовательно ∆КРР₁~∆КММ₁ по двум углам.
Пусть КР=n, тогда РМ=2n (из отношения КР:РМ=1:2), следовательно КМ=KP+PM=n+2n=3n.
Отношение двух любых сторон одного треугольника, равно отношению двух соответствующих сторон треугольника, подобного первому. Тогда:
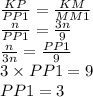
ответ: 3 см
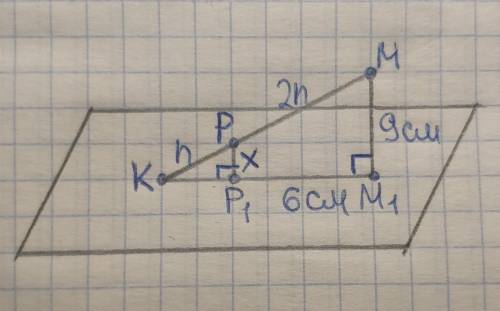
первое
2R sin(&/2) ;2r tg(&/2) ; &- угол с вершиной вцентре тре--ка образованного стороной и ценром ; большой и малыйрадиусы - соответственно. Справедливо для любого правильного мн - ка.
тааакссс второе ты похоже пропустила буковку с когда написала м см ведь имеются ввиду?Я проходила это задание в 9 м классе
1. Во вписанном тр-ке сторона = радиусу = 9.
2. В описанном: высота правильного трка с основанием, = стороне, = 9. Угол при вершине тр-ка = 36. Находи по синусу.
третье
Апофема (от греч. apotithçмi — откладываю в сторону), 1) длина перпендикуляра, опущенного из центра правильного многоугольника на любую из его сторон .
Т.е. высота правильного треугольника со стороной 14. Формула в любом учебнике.
Відповідь:
Дано:
Діагоналі ромба: d₁ = 2 та d₂ = 2√3
У ромба, синус кута між більшою діагоналлю (d₁) та стороною ромба можна знайти за до наступної формули:
sin(θ) = (2 * Площа ромба) / (d₁ * a)
Для знаходження синусу кута, нам потрібно знати площу ромба та довжину однієї з його сторін (a).
Площа ромба може бути знайдена за формулою:
(d₁ * d₂) / 2
Оскільки діагоналі ромба нам вже дані, ми можемо використати ці значення для розрахунку.
Розраховуємо площу ромба:
(2 * 2√3) / 2 = 2√3
Тепер, для знаходження синусу кута, ми повинні знати довжину однієї зі сторін ромба (a). Довжина сторони ромба може бути знайдена за до одного зі співвідношень:
a = (2 * Площа) / d₁
або
a = (2 * Площа) / d₂
Розрахуємо довжину сторони ромба:
a = (2 * 2√3) / 2 = √3
Тепер, використовуючи значення площі (2√3), довжини сторони (√3) та більшої діагоналі (2), ми можемо знайти синус кута:
sin(θ) = (2 * 2√3) / (2 * √3) = 2 / 1 = 2
Отже, синус кута між більшою діагоналлю та стороною ромба дорівнює 2.