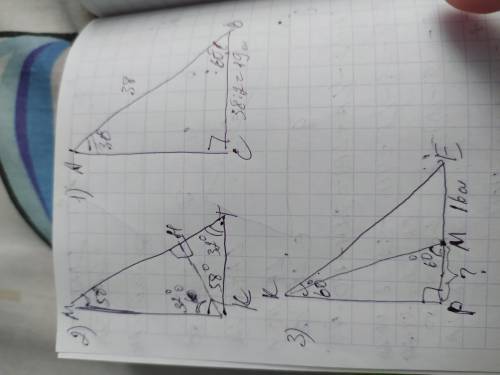
ЗАДАНИЕ 1
В прямоугольном треугольнике сумма острых углов составляет 90°, тогда <А=90-60=30°. Катет лежащий напротив него равен половине гипотенузы поэтому ВС=38/2=19см
ОТВЕТ: ВС=10см
ЗАДАНИЕ 2
Высота КН делит ∆КМТ на 2 прямоугольных треугольника МКН и КТН. Рассмотрим полученный ∆КМН. В нём <МКН=32° и так как сумма острых углов прямоугольного треугольника составляет 90°, то <М=90-32=58°. Также в ∆КМТ, <Т=90-58=32°.
ОТВЕТ: угол Т=32°
ЗАДАНИЕ 3
Сторона КМ образует с катетом МР <КМР=60° и ещё один прямоугольный треугольник КМР. Сумма острых углов прямоугольного треугольника составляет 90°, поэтому <МКР=90-60=30°
Также в ∆РКЕ <Е=90-60=30°.
<МКР=<Е=30°, а катет лежащий напротив него равен половине гипотенузы, поэтому КЕ=2×КР; КМ=2×РМ
Пусть РМ=х, тогда КМ=2х. Найдём КР по теореме Пифагора:
КР²=КМ²-РМ²=(2х)²-х²=4х²-х²=3х²
КР=√3х². Рассмотрим ∆РКЕ. Так как КЕ=2×КР, то КЕ=2√(3х²)
Если РМ=х, тогда РЕ=16+х
Составим уравнение используя теорему Пифагора:
КР²+РЕ²=КЕ²
(√3х²)²+(16+х)²=(2√(3х²))²
3х²+256+32х+х²=4×3х²
4х²+32х+256=12х²
4х²-12х²+32х+256=0
-8х²+32х+256=0 |÷(-8)
х²-4х-32=0
Д=16-4(-32)=16+128=144
х1=(4-12)/2= -8/2= –4
х2=(4+12)/2=16/2=8
х1 = –4 нам не подходит поскольку сторона не может быть отрицательной поэтому используем х2=8
х=РМ=8см
ОТВЕТ: РМ=8см
Полярный угол (угловая координата) для данной точки - это угол, на который нужно повернуть (против часовой стрелки) полярный луч, чтобы данная точка на него попала. При этом радиальная координата данной точки будет показывать расстояние от центра координат до данной точки.
То есть, берем точку на плоскости и делаем ее центром координат. Проводим из нее луч в каком-то направлении в той же плоскости и делаем его полярным лучом (то есть, направлением под углом 0 градусов). Тогда, чтобы определить угловые координаты какой-то произвольной точки на той же плоскости нужно:
1) Повернуть полярный луч против часовой стрелки так, чтобы интересующая точка на него попала. И измерить угол между направлением луча до и после поворота. Это угловая координата.
2) Измерить на повернутом луче расстояние от центра до интересующей точки. Это радиальная координата.
Всё. Полярные координаты определены
Объяснение:
Решение.
Равносторонний треугольник АВС со стороной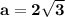 см .
см .
Радиус окружности, вписанной в равносторонний треугольник ,
равен 1/3 высоты , проведённой от вершины к противоположной
стороне ,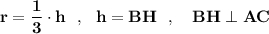 .
.
Длину высоты можно найти из прямоугольного треугольника АВН ,
Радиус вписанной окружности равен
ответ: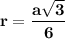 .
.