Відповідь:
До кола з центром у точці О з точки А поза колом проведено дві дотичні AB i AC (точки В і С - точки дотику).Вiдрiзок АО вдвічі більший за радіус кола.
Знайдіть кут ВАС.
Дотичною до кола називається пряма, що має з колом одну спільну точку.
Дотична до кола перпендикулярна радіусу, проведеному до точки дотику.
ВО⟂АВ, СО⟂АС.
=> △АВО і △АСО - прямокутні.
В прямокутному трикутнику катет, що дорівнює половині гіпотенузи, лежить навпроти кута кута 30°.
=> ∠САО=30°.
△АВО=△АСО за гіпотенузою і катетом (АО - спільна, ВО=СО як радіуси).
=> ∠ВАС=∠САО, то ∠ВАС=∠ВАС+∠САО=30°+30°=60°.
=> ∠ВАС=60° => геометричне місце точок рівновiддалених від сторiн кута, є бісектриса цього кута
Пояснення:
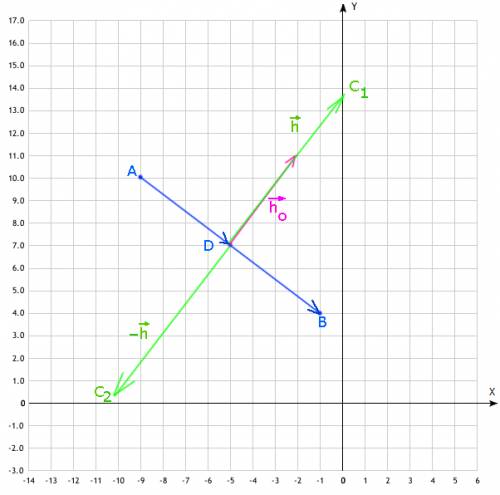
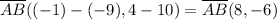 ;
; от точки A
от точки A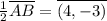 ;
; в обе возможные стороны
в обе возможные стороны перпендикулярен вектору основания
перпендикулярен вектору основания  , а значит его проекции накрест-пропорциональны с противоположным знаком:
, а значит его проекции накрест-пропорциональны с противоположным знаком: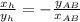 , что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться:
, что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться:  (II) ;
(II) ; пропорционален вектору
пропорционален вектору  , поскольку для вектора
, поскольку для вектора  выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора
выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора  ;
; имеет длину
имеет длину 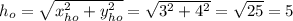 ;
;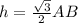 , т.к
, т.к 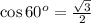 ;
;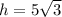 , а стало быть
, а стало быть  ;
;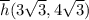 .
.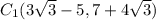 /// примечание:
/// примечание: 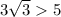 ;
;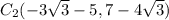 /// примечание:
/// примечание: 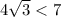 .
.
1.1) угол α-вписанный, значит, дуга AC=2*19=38
2) угол β-вписанный, значит, дуга AB=2*47=94
3) BD- диаметр, CD=180-(дуга АВ+ дуга АС)= 180-(38+94)=180-132=48
4) угол х- вписанный, Значит х=1/2 дуги CD=1/2*48=24
ответ: 24 (рисунок внизу)
2.1х+3х+5х=180
9х=180
х=20
1)20*1=20(1-ый угол)
2)20*3=60(2-ой угол)
3)20*5=100(3-ий угол)
Проверка:
20+60+80=180
3.Если проведем отрезок от другого конца диаметра до этой точки, то мы получим прямоугольный треугольник, так как в нем будет вписанный угол опирающийся на диаметр
1) Найдем диаметр она равен 10*2=20- это будет гипотенузой прямоугольного треугольника
2)по теореме Пифагора:
20²-16²=√400-256=√144=12
ответ:12 см
Объяснение: рисунок относится к первому заданию
Удачи!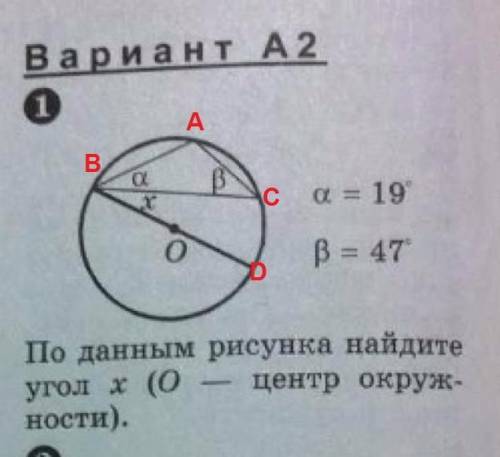
Для розв'язання цієї задачі використаємо теорему про те, що кут між дотичною і радіусом кола, проведеним до точки дотику, є прямим кутом.
Позначимо точку перетину відрізків ВС і АО як К.
Оскільки ОВ = 10 см і кут ВАС = 60º, тоді ОА = ОС = 10 см (Оскільки ОВ - радіус кола).
Оскільки ОА = ОС, то кути ОАК і ОСК також дорівнюють 60º кожен (кути при основі рівнобедреного трикутника).
Отже, трикутник ОАК є рівностороннім.
Також, відповідно до теореми, кути ВАК і САК є прямими кутами.
Тепер розглянемо геометричне місце точок, рівновіддалених від сторін кута ВАС.
Припустимо, що X - точка на геометричному місці. Тоді відстань від X до сторони ВА дорівнює відстані від X до сторони СА.
Оскільки ОАК є рівностороннім трикутником, то ОX = AX.
Також, відстань від X до сторони ВС дорівнює відстані від X до сторони СК.
Оскільки ВС - дотична, то кут ВКС є прямим кутом. Тому відрізок ВК є висотою трикутника ВКС, що проходить через вершину К.
Отже, відрізок ВК є середньою лінією в рівнобедреному трикутнику ВКС і ділить сторону СК навпіл.
З цього випливає, що ОК = КС.
Таким чином, ми довели, що для кожної точки X, розташованої на геометричному місці точок, рівновіддалених від сторін кута ВАС, відрізок ОК є середньою лінією в рівнобедреному трикутнику ОКС і ділить сторону СК навпіл.
Таким чином, геометричне місце точок рівновіддалених від сторін кута ВАС є бісектрисою цього кута.