іть будь-ласка! мені терміново потрібно.. Знайдіть суміжні кути, якщо:
1) Один із них на 20° більший за інший.
2) Один із них у 5 разів менший від іншого.
Задачі розв'язувати рівнянням))

Question

Геометрия: іть будь-ласка! мені терміново потрібно.. Знайдіть суміжні кути, якщо: 1) Один із них на 20° більший за інший. 2) Один із них у 5 разів менший від іншого. Задачі розв язувати рівнянням))

karinaeruslanov · Accepted Answer

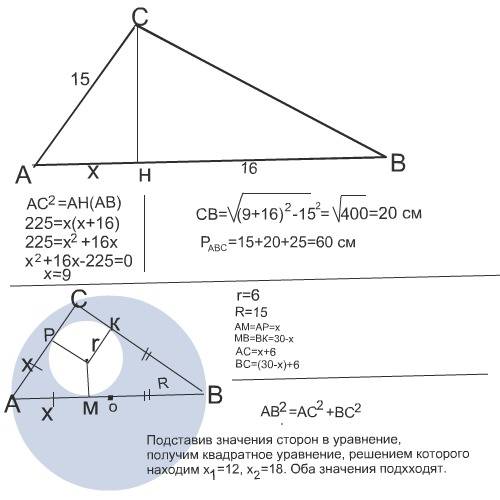
1)Пусть ABC — данный треугольник (угол C — прямой, AC = 15); CD — высота; BD = 16. Обозначим BD = x. Из подобия треугольников ABC и ACD (угол A общий, ⁄ ADC = ⁄ ACB = 90°) получаем

2)

Пусть а и в катеты треугольника, тогда с=30, т.к. радиус описанной окружности равен половине гипотенузы r=p-c,p=r+c=36, P=36*2=72,a+b=72-30=42.имеем

{а+в=42

a^2+b^2=900

{a^2+b^2=2*ab=42^2=1764

a^2+b^2=900

{900+2*ab=1764

2ab=1764-900

{a+b=42

ab=432

a^2-42a+432=0

а1=18,а2=24

в1=24, в2=18

Решить эти : 1)один из катетов прямоугольного треугольника равен 15см, а проекция другого катета на

MOGZ ответил