Чертёж смотрите во вложении.
Дано:
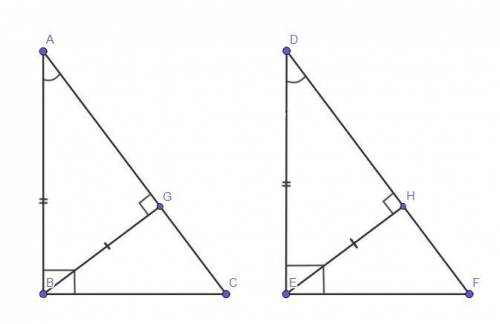
ΔАВС - прямоугольный (∠АВС = 90°).
ΔDEF - прямоугольный (∠DEF = 90°).
ВG - высота ΔАВС.
ЕН - высота ΔDEF.
BG = EH.
Острые ∠ВАС = ∠EDF.
Доказать:
ΔАВС = ΔDEF.
Доказательство:
Рассмотрим ΔBAG и ΔEDH - прямоугольные (так как BG и EH - высоты и они перпендикулярны сторонам, к которым они проведены). Катеты BG = EH по условию (они катеты, так как лежат против острых углов в прямоугольном треугольнике), острые ∠ВАС = ∠EDF по условию, следовательно, прямоугольные ΔBAG = ΔEDH по катету и противолежащему острому углу.
В равных треугольниках против равных углов лежат равные стороны. В прямоугольных ΔBAG и ΔEDH ∠AGB = ∠DHE (так как они прямые), тогда, по выше сказанному, АВ = ED.
Рассмотрим ΔАВС и ΔDEF - прямоугольные. Катеты АВ = ED (по выше доказанному), острые ∠ВАС = ∠EDF (по условию), следовательно, прямоугольные ΔАВС = ΔDEF по катету и прилежащему острому углу.
ответ: что требовалось доказать.
Таким чином, сторона ромба дорівнює m, а менша діагональ ромба дорівнює 2 * (m * sin(a/2)).
Объяснение:
У ромба всі сторони мають однакову довжину, тому сторона ромба також буде мати довжину m.
Гострий кут ромба поділений навпіл його діагоналлю. Отже, можемо розглядати півгострий кут, який дорівнює a/2.
У правильному трикутнику, сторона, що протилежна півгострому куту, дорівнює напівменшій діагоналі ромба.
Таким чином, напівменша діагональ ромба буде рівна m * sin(a/2).
Знаючи напівменшу діагональ, ми можемо знайти меншу діагональ ромба. Для цього потрібно подвоїти значення напівменшої діагоналі:
Менша діагональ = 2 * (m * sin(a/2))
Таким чином, сторона ромба дорівнює m, а менша діагональ ромба дорівнює 2 * (m * sin(a/2)).