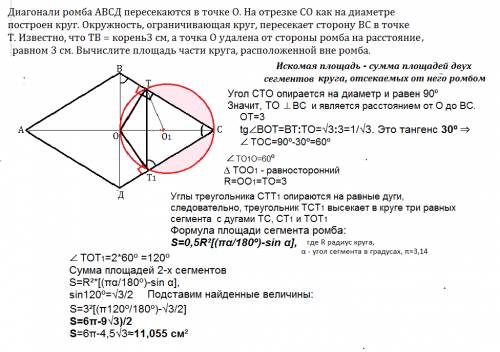
Искомая площадь - сумма площадей двух сегментов круга, отсекаемых от него ромбом.
Угол СТО опирается на диаметр и равен 90º
Расстояние от точки до прямой - длина отрезка из этой точки, перпендикулярного к этой прямой.
ОТ ⊥ ВС и является расстоянием от О до ВС.
ТО=3 см ( расстояние от точки до прямой - перпендикуляр)
Формула площади сегмента ромба:
S=0,5R²[(πα/180º)-sin α],
где R радиус круга, α - угол сегмента в градусах, π≈3,14
∆ ВОС~∆ ВОТ ( прямоугольные с общим углом при В)
∠ВОТ=∠ВСО
tg∠ВОТ=ВТ:ТО=√3:3=1/√3. Это тангенс 30º
∆ ТО1С равнобедренный.
∠ ТСО₁=∠ СТО₁
∠ ТО₁С=180-2∠ТСО₁
Отсюда ∠ТО₁С=180º-2*30º=120º
Из ∆ ТОС
ОС=ТО:sin30º=3:0,5=6 см
R=ОС:2=3 см
Сумма площадей 2-х сегментов
S=R²[(πα/180º)-sin α],
sin 120º=√3/2
Подставим найденные величины:
S=3²[(π120º/180º)-√3/2]
S=6π-9√3)/2
S=6π-4,5√3≈11,055 см²
-------
В приложении решение дано несколько иное, хотя принцип тот же.
Для розв'язання цієї задачі спочатку потрібно з'ясувати, являє собою точка O на колі.
Оскільки CD є діаметром кола, то точка O є серединою відрізка CD. Отже, CO = DO = CD / 2 = 12 см / 2 = 6 см.
Тепер ми можемо побудувати трикутник AOC, в якому ми знаємо сторону AC = 5 см і сторону CO = 6 см.
Для знаходження периметра ∆AOC потрібно просумувати довжини всіх трьох сторін трикутника AOC.
Периметр трикутника обчислюється за формулою: периметр = сторона1 + сторона2 + сторона3.
У нашому випадку, сторона1 = AC = 5 см, сторона2 = CO = 6 см.
Щоб знайти сторону3, ми можемо скористатися властивістю кола, що каже, що будь-який радіус кола перпендикулярний до дотичної. Отже, ∆AOC є прямокутним трикутником, і сторона3 = AO.
Так як AO є радіусом кола, то AO = CO = 6 см.
Тепер ми можемо обчислити периметр ∆AOC:
Периметр = сторона1 + сторона2 + сторона3
Периметр = AC + CO + AO
Периметр = 5 см + 6 см + 6 см
Периметр = 17 см.
Периметр трикутника ∆AOC дорівнює 17 см.