1)
Знайдіть периметр паралелограма, сторони якого дорів-нюють 4 см і 6 см.
2)
Один із кутів ромба дорівнюе 50°. Знайдіть інші кути
ромба.
3)
Знайдіть площу трикутника, одна зі сторін якого дорів-не 3 дм, а висота, що проведена до ції сторони, - 8 дм.
4)
Середня лінія трапеції дорівнюе 9 см. Знайдіть основи трапеції, якщо одна з них на 2 см менша від іншої.
5)
Трикутники ABC і 4,B,C, подібні. Знайдіть неві-домі сторони трикутників, якщо ВС = 4 см; АС = 3 см;
B,C, = 12 см; A,B, = 15 см.
6)
Катети прямокутного трикутника дорівнюють
40 см
і 18 см. Знайдіть довжину медіани, проведеної до мен-
шого катета.
7)
У ДАВС трикутник (кути трикутника знайдіть із точністю до градусів).
8)
Точка дотику кола, вписаного у рівнобічну трапецію, ді-лить бічну сторону на відріки 3 см і 27 см. Знайдіть площу трапеції
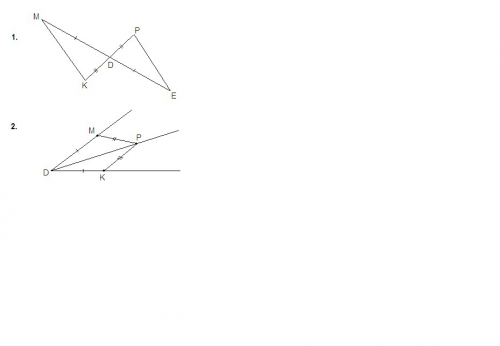
PD = DK по условию,
∠MDK = ∠EDP как вертикальные, ⇒
ΔMDK = ΔEDP по двум сторонам и углу между ними.
В равных треугольниках напротив равных сторон лежат равные углы, значит
∠KMD = ∠PED.
2. DM = DK по условию,
РМ = РК по условию,
DP - общая сторона для треугольников DMP и DKP, ⇒
ΔDMP = ΔDKP по трем сторонам.
В равных треугольниках напротив равных сторон лежат равные углы, значит ∠MDP = ∠KDP, следовательно
DP - биссектриса угла D.
3. Начертим окружность с центром в точке А произвольного радиуса (большего, чем расстояние до прямой ВС). Точки пересечения этой окружности с прямой ВС - К и М.
Начертим две окружности одинакового произвольного радиуса (большего половины отрезка КМ) с центрами в точках К и М.
Через точки пересечения этих окружностей (Е и F) проводим прямую.
EF ∩ BC = H. АН - искомая высота.
Прямая EF всегда пройдет через точку А, так как является серединным перпендикуляром к отрезку КМ, а точка А равноудалена от концов этого отрезка, а значит лежит на серединном перпендикуляре.