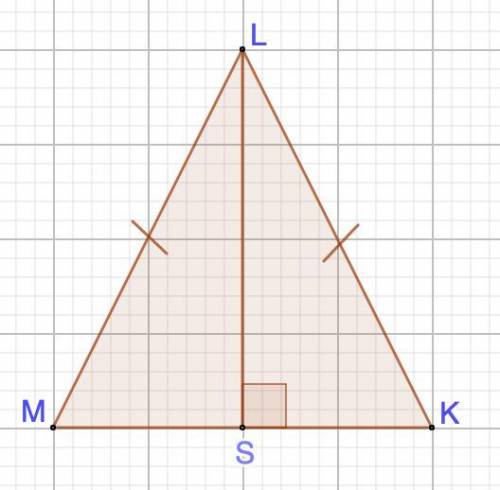
Объяснение:
Дано: ΔLMK - равнобедренный.
МК - основание.
LS - высота
Доказать: ΔLSM = ΔLSK, используя 2 и 3 признаки равенства треугольников.
Доказательство:
1) 2 признак равенства треугольников:
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники называются равными.
Рассмотрим ΔLSM и ΔLSK - прямоугольные (LS - высота)
⇒ ∠LSM = ∠LSK = 90°
В равнобедренном треугольнике высота является биссектрисой.
⇒ ∠MLS = ∠SLK
LS - общая
⇒ ΔLSM = ΔLSK (по 2 признаку)
2) 3 признак равенства треугольников:
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники называются равными.
Рассмотрим ΔLSM и ΔLSK - прямоугольные (LS - высота)
В равнобедренном треугольнике высота является медианой.
⇒ MS = SK
ML = LK (ΔLMK - равнобедренный)
LS - общая
⇒ ΔLSM = ΔLSK (по 3 признаку)
Точка касания окружности вписанной в равнобедренную трапецию делит ее боковую сторону на отрезки длиной 9 см и 16 см. Найдите площадь трапеции
Объяснение:
АВСD-трапеция АВ=СD, точки касания расположены на сторонах
А-Е-В, В-К-С, С-Т-D, А-Н-D ,АЕ=16 см, ЕВ=9 см.
АВ=16+9=25 см. Значит СD=25 см.
S(трап.)= 1/2*Р*r , r-радиус вписанной окружности .
По свойству отрезков касательных АЕ=АН=DT=DH=16 см и
ВК=ВЕ=СК=СТ=9 см.
Р=25+25+(9+9)+(16+16)=100 (см)
Радиус вписаной окружности равен половинге высоты трапеции.
Пусть ВМ⊥АD ,ΔАВМ-прямоугольный , по т. Пифагора ВМ=√(25²-7²)=√576=24 (см)
Тогда r=1/2*24=12(см).
S(трап.)=1/2*100*12=600 (см²)