Плоский угол при вершине правильной треугольной пирамиды равен 90°.
Найти отношение боковой поверхности этой пирамиды к площади ее основания.
Площадь правильного треугольника - а основание правильной пирамиды - правильный треугольник
S=(a²√3):4
Площадь боковой поверхности - это площадь трех граней пирамиды.
Каждая грань - равнобедренный треугольник с основанием а, равным стороне правильного треугольника в основании пирамиды, и высотой h=апофеме.
S=ah:2
Чтобы найти площадь боковой поверхности, нужно найти апофему.
Угол АSC- прямой.
Треугольник ASC - прямоугольный равнобедренный.
Апофема грани пирамиды - высота и медиана этого треугольника.
Медиана прямоугольного треугольника равна половине гипотенузы.
Высота SM равна половине АС и равна а:2
Площадь треугольника АSС=(а*а:2):2=а²:4
Площадь боковой поверхности равна 3а²:4
Отношение боковой поверхности этой пирамиды к площади ее основания
Sбок:S ᐃ АВС=(3а²:4):{(a²√3):4}=√3
ответ:√3/3
* * *
Косинус угла- отношение катета, прилежащего к углу, к гипотенузе.
Нужный угол равен линейному углу двугранного угла между данными плоскостями. Линейным углом двугранного угла называется угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.
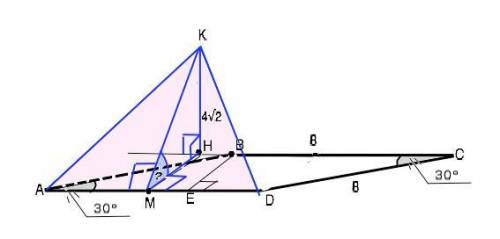
Сделаем и рассмотрим рисунок, соответствующий условию задачи. КН - расстояние от т.К до плоскости ромба. ВЕ - высота ромба. cos ∠КМН - искомый.
ВЕ⊥АD=АВ•sin30°=8•1/2=4 см.
КН⊥ВС, НМ⊥АD, НМ=ВЕ=4 см ( расстояние между параллельными прямыми равно в любой точке)
По т. о 3-х перпендикулярах КМ⊥АD. Т.к. ∆ АКD правильный, его углы равны 60°.⇒ КМ=АК•sin60°=4√3 или по т.Пифагора из ∆ КНМ получим тот же результат. ⇒ cos∠KMH=МН/КМ=4/4√3=1/√3 или иначе √3/3
9.589 см²
Объяснение:
Для розв'язання цієї задачі використаємо формулу для обчислення площі бічної поверхні тетраедра. Площа бічної поверхні тетраедра може бути обчислена за до формули Герона, яка базується на довжинах його бічних ребер.
Спочатку виміряємо довжину трьох бічних ребер тетраедра, які в даному випадку дорівнюють 4 см, 5 см і 6 см.
Застосуємо формулу Герона для обчислення площі бічної поверхні тетраедра:
Площа = √[s(s-a)(s-b)(s-c)],
де s - півпериметр трикутника, a, b, c - довжини сторін трикутника.
Спочатку знайдемо півпериметр (s) трикутника, використовуючи довжини бічних ребер:
s = (a + b + c) / 2
s = (4 + 5 + 6) / 2 = 15 / 2 = 7.5
Підставимо значення s, a, b, c в формулу для обчислення площі:
Площа = √[7.5(7.5-4)(7.5-5)(7.5-6)]
Площа = √[7.5(3.5)(2.5)(1.5)]
Площа ≈ √[91.875]
Площа ≈ 9.589 см²
Отже, площа бічної поверхні тетраедра становить приблизно 9.589 см².