
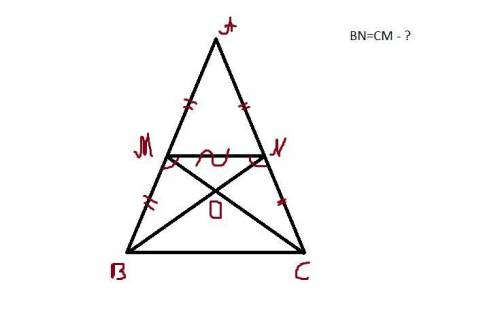
Т.к. АВ=АС , то треугольник равнобедренный
Прямая MN - средняя линия треугольника, значит она разбивает стороны АВ и АС на равные отрезки, которые также равны между собой
Прямая MN отделяет от треугольника АВС равнобокую трапецию BMNC с диагоналями BN и МС. А т.к. трапеция равнобокая, то ее диагонали равны, т.е. BN = МС, ч.т.д.
Или же можно продолжить доказывать равенство этих прямых через ПРТ (треугольники на рассмотрение: BMN и CNM). У них MN - общая сторона; BM=NC и ∠BMN = ∠CNM (как односторонние углы равнобокой трапеции). Отсюда ΔBMN = ΔCNM по 1 ПРТ, значит, BN = МС, ч.т.д.
Точка B(3,-2,2)
а) параллельна плоскости Oyz.
Уравнение плоскости, параллельной плоскости yOz, имеет вид: Ax + D = 0.
Подставляя в него координаты точки A, получим 3A + D = 0, или D = -3A.
Подставляя это значение в Ax + D = 0, получим
Ax - 3A = 0,
а сокращая на A, будем иметь окончательно
x - 3 = 0.
б) перпендикулярна оси Ox.
Так как плоскость перпендикулярна оси Ox, то она параллельна плоскости yOz, а потому ее уравнение имеет вид
Ax + D = 0.
Подставляя в это уравнение координаты точки A, получим, что D = -3A. Это значение D подставим вAx + D = 0 и, сокращая на A, будем иметь окончательно x - 3 = 0.
Подробнее - на -
ответ: 80 градусам
Объяснение:
во вложении