
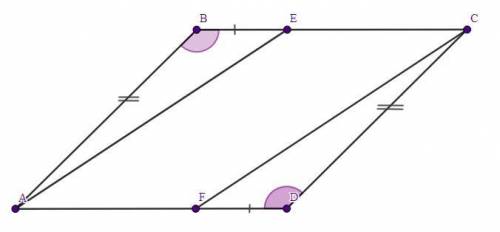
Четырёхугольник ABCD - параллелограмм.
ВЕ = DF (Е ⊂ ВС, F ⊂ AD).
Доказать :Четырёхугольник AECF - параллелограмм.
Доказательство :В параллелограмме противоположные углы и противоположные стороны равны между собой (свойство параллелограмма).Отсюда следует, что ∠В = ∠D, АВ = CD.
Рассмотрим ΔАВЕ и ΔCDF.
ВЕ = DF (по условию)
∠В = ∠D, АВ = CD (по выше сказанному) ⇒ ΔАВЕ = ΔCDF по двум сторонам и углу между ними (первый признак равенства треугольников).
Из равенства треугольников следует и равенство сторон АЕ и CF.
AD = BC (по свойству параллелограмма), но в своё очередь AD = BE + EC ; BC = DF + AF. Учитывая равенство из условия получаем, что ЕС = AF.
Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник - параллелограмм (свойство параллелограмма).АЕ = CF ; ЕС = AF (по выше сказанному) ⇒ четырёхугольник AECF - параллелограмм.
ответ :Что требовалось доказать.
Для знаходження площі рівнобічної трапеції можна використовувати наступну формулу:
S = ((a + b) / 2) * h
де a та b - основи трапеції, а h - висота трапеції.
Оскільки трапеція є рівнобічною, то її бічні сторони теж мають довжину 6 см, що дозволяє визначити її висоту за формулою:
h = a / 2 * sqrt(2) = 24 см / 2 * sqrt(2) ≈ 8,49 см
Отже, за формулою для площі трапеції:
S = ((a + b) / 2) * h = ((24 см + 6 см) / 2) * 8,49 см ≈ 127,35 см²
Отже, площа рівнобічної трапеції дорівнює близько 127,35 см².