Для любой правильной призмы справедливы формулы:
Площадь боковой поверхности:
Sбок = Pосн · h, где
Росн - периметр основания,
h - высота.
Площадь полной поверхности:
Sполн = Sбок + 2Sосн
Объем:
V = Sосн · h
____________________
a - сторона основания.
____________________
Правильная треугольная призма:
в основании лежит правильный треугольник, значит
Sосн = 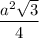
Sбок = 3а · h
Sполн = 3a · h + 2 · a²√3/4 = 3ah + a²√3/2
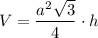
____________________
Правильная четырехугольная призма:
в основании - квадрат, значит
Sосн = a²
Sбок = 4ah
Sполн = 4ah + 2a²
V = a²h
____________________
Правильная шестиугольная призма:
Sосн = 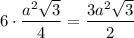
Sбок = 6ah
Sполн = 6ah + 2 · 3a²√3/2 = 6ah + 3a²√3
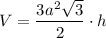
1. В правильному семикутнику кількість внутрішніх кутів дорівнює 7. Формула для знаходження суми внутрішніх кутів дорівнює: S=(n-2)*180, де n - кількість кутів. Значить, для правильного семикутника: S=(7-2)*180=900 градусів. Оскільки всі кути правильного семикутника однакові, то кожен кут дорівнює 900/7≈128,6 градусів.
2. Площа прямокутного трикутника дорівнює (a*b)/2, де a та b - його катети. Тому, знаючи, що площа дорівнює 24 см², а один катет рівний 8 см, можна знайти другий катет:
(8*b)/2=24, тобто b=6.
Для знаходження гіпотенузи застосовуємо теорему Піфагора:
c²=a²+b².
Отже, c²=8²+6²=100.
Складаємо квадратні корені обох боків рівняння:
c=10 см.
Отже, другий катет дорівнює 6 см, а гіпотенуза - 10 см.