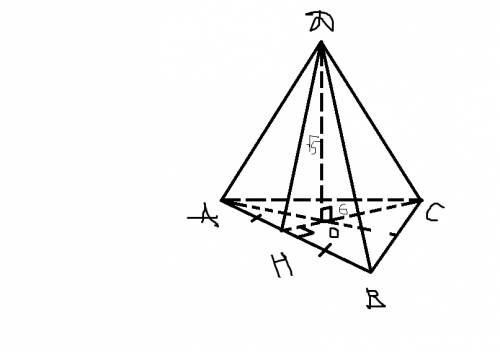
Рассмотрим треугольниу ABC-равносторонний(т.к.DABCD-прав. пирамида) OH=CH/3=6/3=2 (см)(в точке пересечения медианы делятся в отношении 2:1 от вершины)
Рассм. треуг. ODH-прямоуг. По теореме Пифагора DH=корень из DO^2+OH^2=корень из 5+4=корень из 9=3 (см)
Sпп=Sбп+Sосн
Рассм. треуг BCH-прямоуг.
sinB=MC/BC
sin60=6/BC
BC=6/(корень из 3/2)(под корнем только 3)=12/корень из 3=12 корней из 3/3=4 корня из 3(см)
Pосн=3*4 корня из 3=12 корней из 3 (см)
Sбп=1/2*DH*Pосн
Sбп=1/2*3*12 корней из 3=18корней из 3(см^2)
Sосн=1/2*CH*AB=1/2*6*4 корня из 3=12корней из3 (см^2)
Sпп=18корней из 3+12 корней из 3= 30 корней из3 (см^2)
1. Угол между наклонной к плоскости и плоскостью - это угол между наклонной и ее проекцией на плоскость. Искомый угол - угол МАО. Высота правильного треугольника равна h=(√3/2)*a = (√3/2)*2√3=3. АО=(1/3)*h = 1 (свойство медианы). Tg(<MAO) = MO/AO = √3.
ответ: α = arctg√3 = 60°
2. Искомый угол - угол между наклонной и ее проекцией, то есть угол АВК. Sin(<ABK) = KA/KB = AC*tg60/5 = 5√3/11. <ABK = arcsin(0,787) ≈ 51,9°.
3. Опустим перпендикуляры SP и SH из точки S к сторонам АВ и АD соответственно. Прямоугольные треугольники APS и AHS равны по гипотенузе и острому углу. Значит АР=АН и АРОН - квадрат. тогда АО = АН*√2 (диагональ квадрата), АS = 2*АН (в треугольнике ASH катет АН лежит против угла 30°, а AS - гипотенуза). Косинус искомого угла (между наклонной AS и плоскостью АВСD, равного отношению проекции наклонной к наклонной) = АО/AS = АН√2/(2*АН) = √2/2.
ответ: искомый угол равен 45°.